Navegación
Propiedades de las integrales indefinidas
De Wikillerato
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| - | Por la definición, | + | Por la definición, la derivada de la función integral indefinida es igual a la función integrando: |
| - | función integrando: | + | |
<br/> | <br/> | ||
| Línea 16: | Línea 15: | ||
<br/> | <br/> | ||
| - | La integral de la suma de dos funciones es igual a la suma de las integrales de las | + | La integral de la suma de dos funciones es igual a la suma de las integrales de las funciones: |
| - | funciones: | + | |
<br/> | <br/> | ||
| Línea 36: | Línea 34: | ||
<br/> | <br/> | ||
| - | La integral indefinida del producto de un | + | La integral indefinida del producto de un número real <math> k </math> por una función es igual al producto de <math> k </math> por la integral indefinida de la función: |
| - | <math> | + | |
| - | k | + | |
| - | </math> | + | |
| - | por una función es igual al producto de | + | |
| - | <math> | + | |
| - | k | + | |
| - | </math> | + | |
| - | por la integral indefinida de la función: | + | |
<br/> | <br/> | ||
Revisión de 19:05 10 mar 2008
Por la definición, la derivada de la función integral indefinida es igual a la función integrando:
![\left[
</p>
<pre> \, \int \mathrm{f} \left( \, x \, \right) \mathrm{d}x \,
</pre>
<p>\right]
^\prime \, = \, \mathrm{f} \left( \, x \, \right)](/images/math/math-c06a2d0283cdfe91518030ef55eefff0.png "\left[
</p>
<pre> \, \int \mathrm{f} \left( \, x \, \right) \mathrm{d}x \,
</pre>
<p>\right]
^\prime \, = \, \mathrm{f} \left( \, x \, \right)")
La integral de la suma de dos funciones es igual a la suma de las integrales de las funciones:
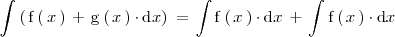
La integral indefinida del producto de un número realpor una función es igual al producto de
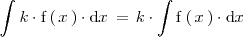
Para demostrar las ultimas dos igualdades basta con derivar los dos terminos en ambas igualdades.
Tweet
