Fuerzas y Sistemas Materiales

De Wikillerato

Revisión de 07:31 14 abr 2008

Interacciones mecánicas

Si revisamos algunos de los casos vistos al estudiar la naturaleza de las fuerzas, veremos como, en cada caso, existe una interacción entre el cuerpo y la acción aplicada sobre él.

Si suspendemos una masa por el extremo de un hilo inextensible, y sujetamos con los dedos el otro extremo, aparecen sendas interacciones entre la masa y el hilo por un lado y entre el hilo y la mano por otro. A la fuerza que tira de la masa hacia abajo, su Peso, se opone el hilo con la tensión que sufre 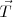. Pero 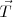es consecuencia de que el hilo sea inextensible, y sin romperse. Se encuentra sobre cada punto del hilo – si lo cortamos, la masa cae pero el hilo pierde la forma vertical porque 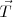deja de existir-. También en el extremo que sujetamos con la mano, nosotros ejercemos una fuerza igual y de signo opuesto, es decir hacia arriba, a la tensión en ese punto.

Si soltamos, la tensión desaparece. No hay pues tensiones negativas, la tensión existe o no existe, y por lo tanto, si existe, su signo es positivo. Sin embargo, si adoptamos como criterio de signos que la tensión con sentido hacia arriba es positiva, cuando vaya hacia abajo será negativa. En cualquier punto del hilo, salvo en los extremos, estarán presentes ambos vectores de modo que su suma sea cero, pero hablaremos de la Tensión, de una sola.

Si queremos estudiar las interacciones de un modelo separado aislamos la parte del sistema a estudiar, como se señala con las líneas roja y azul, respectivamente. En los extremos del hilo tendremos .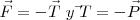

Cuando suspendemos una masa de un resorte, que se encuentre suspendido de una barra horizontal en el sistema existen interacciones entre la masa y el resorte y el resorte y la varilla.

La masa ejerce una acción sobre el resorte igual a su peso P , por su parte el resorte se opone a su alargamiento con su fuerza elástica, hasta que, al llegar al equilibrio,esa fuerza se hace igual al peso pero con sentido opuesto, es decir, hacia arriba. Por su parte el resorte, por el extremo superior, actúa sobre la varilla con una acción igual a su fuerza elástica. Si la varilla es indeformable, ésta actúa sobre el resorte con una fuerza igual y de sentido opuesto, pues de lo contrario la varilla cedería.

Del mismo modo cuando estudiamos el sistema formado por el cilindro y la mesa, colegimos que el cilindro es sostenido por el tablero pues de lo contrario caería al suelo.

El cilindro ejerce una acción sobre la mesa igual a su peso 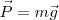, que es vertical. El tablero debe ejercer una fuerza igual de sentido contrario, Fuerza de Reacción, R, perpendicular al plano de la mesa, que se encontrará distribuida entre todos los puntos de la base del cilindro.

Hasta aquí hemos visto algunos ejemplos de las interacciones de las fuerzas de contacto, pero ¿Qué ocurre con las fuerzas a distancia? ¿Por qué un cuerpo cae hacia la Tierra y por qué la Luna evoluciona alrededor de la Tierra sin precipitarse sobre nosotros?¿Por qué la Tierra evoluciona alrededor del Sol y no continua su viaje espacial en línea recta?

La Tierra ejerce una fuerza sobre todos los cuerpos que depende de su masa respectiva, de la distancia a cada cuerpo y de la masa de la Tierra. Esa fuerza es muy grande con relación a la masa de cada cuerpo y la acción que ejerce la Tierra les obliga a precipitarse sobre el suelo. Sin embargo esa fuerza es muy pequeña para desplazar a la Tierra de su posición o desviar su trayectoria.

La Tierra atrae a la Luna con una acción tal que sólo, y nada menos, puede hacer variar la dirección de su movimiento, obligándola a evolucionar alrededor de la Tierra. La Luna ejerce una fuerza igual y de signo contrario sobre la Tierra, pero la masa de la tierra es muy grande para desviar su trayectoria, sin embargo, como se verá, sí que influye sobre la altura de las mareas.

La acción que ejerce la Tierra sobre la Luna, 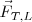, es igual y de sentido opuesto a la reacción de la Luna sobre la tierra,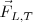

Ambas fuerzas se encuentran aplicadas sobre el centro de la Luna y de la Tierra, respectivamente, y su dirección es la de la línea que los une.

Del mismo modo podemos plantear la existencia de dos fuerzas iguales y de sentido opuesto cuando se trata de fuerzas eléctricas que son también fuerzas a distancia.