Teorema de Rouche-Fröbenius
De Wikillerato
| Línea 1: | Línea 1: | ||
| - | + | {{revisar}} | |
| - | + | <br> | |
| - | <br | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
[[Imagen:frobenius.jpg|frame|Georg F. Fröbenius fue un matematico aleman que nacio en | [[Imagen:frobenius.jpg|frame|Georg F. Fröbenius fue un matematico aleman que nacio en | ||
1849 y murio en 1917. ¡Gracias Georg por tu legado!]] | 1849 y murio en 1917. ¡Gracias Georg por tu legado!]] | ||
| - | + | ==Enunciado== | |
| - | Un [[Sistemas de ecuaciones lineales|sistema]] de | + | {{teorema|1=Un [[Sistemas de ecuaciones lineales|sistema]] de |
<math> | <math> | ||
m | m | ||
| Línea 20: | Línea 14: | ||
n | n | ||
</math> | </math> | ||
| - | | + | incógnitas es compatible (tiene solución) si, y sólo si, el [[Rango de una matriz|rango]] de la matriz de los coeficientes coincide con el rango de la matriz |
| - | ampliada. | + | ampliada.|2=[[Rouche-Fröbenius]]}} |
| - | + | ||
| - | + | ||
Si el sistema es compatible, existen dos posibilidades: | Si el sistema es compatible, existen dos posibilidades: | ||
| - | + | # Que el rango de la matriz de los coeficientes sea menor que el numero de incógnitas. | |
| - | + | # Que el rango de la matriz de los coeficientes sea igual al numero de incognitas. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
En el primer caso el sistema es [[Tipos de sistemas de ecuaciones lineales|compatible | En el primer caso el sistema es [[Tipos de sistemas de ecuaciones lineales|compatible | ||
| Línea 41: | Línea 26: | ||
[[Tipos de sistemas de ecuaciones lineales|compatible determinado]]. | [[Tipos de sistemas de ecuaciones lineales|compatible determinado]]. | ||
| - | |||
==Ejemplo:sistemas homogeneos== | ==Ejemplo:sistemas homogeneos== | ||
| - | |||
En un sistema de ecuaciones homogeneo, la matriz | En un sistema de ecuaciones homogeneo, la matriz | ||
| Línea 58: | Línea 41: | ||
podemos obtener una solución particular igualando todas las incognitas a 0. | podemos obtener una solución particular igualando todas las incognitas a 0. | ||
| - | |||
Un sistema homogeneo es compatible indeterminado cuando el determinante de la matriz de | Un sistema homogeneo es compatible indeterminado cuando el determinante de la matriz de | ||
los coeficientes es cero. Si este determinante no es cero el sistema homogeneo es | los coeficientes es cero. Si este determinante no es cero el sistema homogeneo es | ||
compatible determinado. | compatible determinado. | ||
| - | |||
| - | |||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 14:13 12 ago 2008
Este artículo o sección necesita una revisión de gramática, ortografía o estilo.
Cuando se haya corregido, borra esta plantilla, por favor.
Enunciado
|
Si el sistema es compatible, existen dos posibilidades:
- Que el rango de la matriz de los coeficientes sea menor que el numero de incógnitas.
- Que el rango de la matriz de los coeficientes sea igual al numero de incognitas.
En el primer caso el sistema es compatible indeterminado y en el segundo caso el sistema es compatible determinado.
Ejemplo:sistemas homogeneos
En un sistema de ecuaciones homogeneo, la matriz
 de los terminos independientes es una matriz nula, de manera que el
rango de la
matriz de los coeficientes y el de la
matriz ampliada coinciden. Esto implica, a su vez, por el teorema de Rouché-Fröbenius,
que un sistema homogeneo siempre es compatible. En cualquier sistema homogeneo, siempre
podemos obtener una solución particular igualando todas las incognitas a 0.
de los terminos independientes es una matriz nula, de manera que el
rango de la
matriz de los coeficientes y el de la
matriz ampliada coinciden. Esto implica, a su vez, por el teorema de Rouché-Fröbenius,
que un sistema homogeneo siempre es compatible. En cualquier sistema homogeneo, siempre
podemos obtener una solución particular igualando todas las incognitas a 0.
Un sistema homogeneo es compatible indeterminado cuando el determinante de la matriz de
los coeficientes es cero. Si este determinante no es cero el sistema homogeneo es



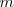 ecuaciones lineales con
ecuaciones lineales con
 incógnitas es compatible (tiene solución) si, y sólo si, el
incógnitas es compatible (tiene solución) si, y sólo si, el 
