Asíntotas
De Wikillerato
Tabla de contenidos |
Introducción
Las asíntotas de una funcíon son rectas a las que "se aproximan" su gráfica.
En los siguientes apartados concretaremos que se entiende por "se aproximan".
Asíntotas verticales
Se dice que la recta vertical de ecuación

es una asíntota vertical de la función
 ,
si y solo si
,
si y solo si
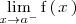
es
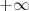 o
o
 ,
o bien
,
o bien
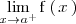
es
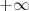 o
o
 .
.
No hay limite al número de asíntotas verticales que puede tener una función.
Ejemplos
Ejemplo 1
La función
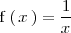 tiene una asíntota vertical de ecuación
tiene una asíntota vertical de ecuación
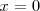
ya que
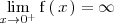
y
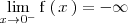
Notese que la asíntota vertical de esta función es el eje Y.
Ejemplo 2
La función
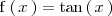 tiene una asíntota vertical de ecuación
tiene una asíntota vertical de ecuación
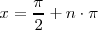
para cada
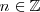 .
.
Por lo tanto, tiene infinitas asíntotas verticales.
Asíntota vertical y gráfica
A la hora de dibujar en la gráfica una asíntota vertical de ecuacion
 ,
es importante conocer ambos limites laterales:
,
es importante conocer ambos limites laterales:
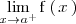 y
y
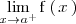
Veamos varios ejemplos en los que se ve claramente los distintos tipos de asíntotas verticales que se pueden tener dependiendo de como sean los limites laterales anteriores.
Ejemplos
Ejemplo 1
A la izquierda y a la derecha de la asíntota vertical la función tiende a
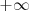 .
.
Ejemplo 2
A la izquierda y a la derecha de la asíntota vertical la función tiende a
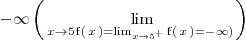 .
.
Ejemplo 3
A la izquierda de la asíntota vertical la función tiende a
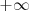 y a la derecha a
y a la derecha a
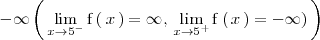 .
.
Ejemplo 4
A la izquierda de la asíntota vertical la función tiende a
 y a la derecha a
y a la derecha a
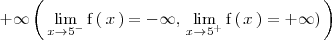 .
.
Ejemplo 5
A la izquierda de la asíntota vertical la función tiende a un punto en la
asíntota vertical
y a la derecha la función tiende a
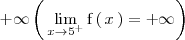 .
.
Asíntotas horizontales
La función
 tiene una asíntota horizontal por la derecha de ecuación
tiene una asíntota horizontal por la derecha de ecuación
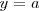 si y solo si
si y solo si
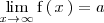
La función
 tiene una asíntota horizontal por la izquierda de ecuación
tiene una asíntota horizontal por la izquierda de ecuación
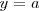 si y solo si
si y solo si
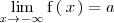
Pueden darse los siguientes casos:
- 1. No existe ninguna asíntota horizontal.
- 2. Existe una unica asíntota horizontal por la derecha pero no existe asíntota
horizontal por la izquierda.
- 3. Existe una unica asíntota horizontal por la izquierda pero no existe asíntota
horizontal por la derecha.
- 4. Existen dos asíntotas horizontales, una por la izquierda y otra por la derecha.
En este ultimo caso, las asíntotas horizontales por la derecha y por la izquierda pueden coincidir, pero, en general, no tienen porque coincidir.
Ejemplos
Ejemplo 1
La función
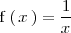 tiene una asíntota horizontal de ecuación
tiene una asíntota horizontal de ecuación
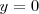
ya que
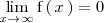
y
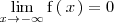
En este caso la asíntota horizontal por la izquierda y por la derecha coinciden ( ambas son el eje X ).
Ejemplo 2
Gráfica de una función con asíntota horizontal por la izquierda:
Ejemplo 3
Gráfica de una función con asíntota horizontal por la derecha:
Ejemplo 4
Gráfica de una función con asíntotas horizontales por la derecha y por la izquierda:
Asíntotas oblicuas
Si
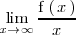
es un número real
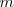 distinto de cero diremos que la función
distinto de cero diremos que la función
 tiene una asíntota oblicua por la derecha.
tiene una asíntota oblicua por la derecha.
En este caso, la asíntota oblicua por la derecha es la recta de ecuación
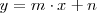
donde
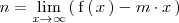
Si
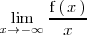
es un número real
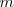 distinto de cero diremos que la función
distinto de cero diremos que la función
 tiene una asíntota oblicua por la izquierda.
tiene una asíntota oblicua por la izquierda.
En este caso, la asíntota oblicua por la izquierda es la recta de ecuación
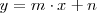
donde
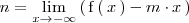
Pueden darse los siguientes casos:
- 1. No existe ninguna asíntota oblicua.
- 2. Existe una unica asíntota oblicua por la derecha pero no existe asíntota
oblicua por la izquierda.
- 3. Existe una unica asíntota oblicua por la izquierda pero no existe asíntota
oblicua por la derecha.
- 4. Existen dos asíntotas oblicuas, una por la izquierda y otra por la derecha.
En este ultimo caso, las asíntotas oblicuas por la derecha y por la izquierda pueden coincidir, pero, en general, no tienen porque coincider.
Si por la derecha ( izquierda ) existe asíntota horizontal, no existe asíntota oblicua y viceversa.
Es decir, no puede darse el caso que una función tenga asíntotas horizontal y oblicua por la derecha ( izquierda ).
Ejemplos
Ejemplo 1
Gráfica de una función con asíntotas oblicuas por la derecha y por la izquierda.
Ejemplo 2
Sea
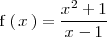
Como
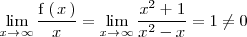
La función
 tiene una asíntota oblicua por la derecha de pendiente 1.
tiene una asíntota oblicua por la derecha de pendiente 1.
Para calcular su ordenada en el origen
 calculamos el siguiente limite
calculamos el siguiente limite
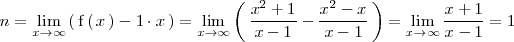
Por tanto la ecuación de la asíntota oblicua por la derecha es
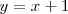
Como
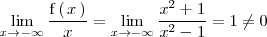
La función
 tiene una asíntota oblicua por la izquierda de pendiente 1.
tiene una asíntota oblicua por la izquierda de pendiente 1.
Para calcular su ordenada en el origen
 calculamos el siguiente limite
calculamos el siguiente limite
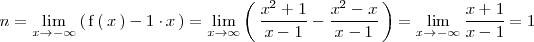
Por tanto la ecuación de la asíntota oblicua por la izquierda es tambien
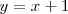
En este ejemplo, las asíntotas oblicuas por la izquierda y por la derecha coinciden.
Tweet


