Métodos de resolución de sistemas de ecuaciones lineales
De Wikillerato
Tabla de contenidos |
Introducción
Método de reducción
Consiste en multiplicar ecuaciones por numeros y sumarlas para reducir el número de incognitas hasta llegar a ecuaciones con solo una incognita.
Multiplicar una ecuación por un número consiste en multiplicar ambos miembros de la ecuación por dicho número que no existe
Sumar dos ecuaciones consiste en obtener una nueva ecuación cuyo miembro final, debe ser igual a 0, para poder eliminar la incognita
Ejemplo
Multiplicando la primera ecuación por 3 y la segunda por -5, se obtienen las ecuaciones
15x - 9y = 6 -15x + 20y = 5
Al sumar ambas ecuaciones nos da la ecuación
11y = 11 </math> </center>
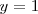 </center>
La elección de los factores 3 y -5 se ha hecho precisamente para que la
</center>
La elección de los factores 3 y -5 se ha hecho precisamente para que la
 desaparezca al sumar ambas ecuaciones.
desaparezca al sumar ambas ecuaciones.
Sutituyendo 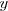 por uno en la primera ecuación del sistema de
ecuaciones de partida, se obtiene
por uno en la primera ecuación del sistema de
ecuaciones de partida, se obtiene
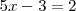
que es otra ecuación con una sola incognita y cuya solución es
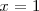 .
.
Texto en negrita'Texto en cursiva
Método de igualación
Método de sustitución
Método de Gauss
El método de Gauss consiste en transformar el sistema dado en otro equivalente. Para ello tomamos la matriz ampliada del sistema y mediante las operaciones elementales con sus filas la transformamos en una matriz triangular superior ( o inferior ). De esta forma obtenemos un sistema equivalente al inicial y que es muy facil de resolver.
Es esencialmente el método de reducción. En el método de Gauss se opera con ecuaciones, como se hace en el método de reducción, pero uno se ahorra el escribir las incognitas porque al ir los coeficientes de una misma incognita siempre en una misma columna, uno sabe en todo momento cual es la incognita a la que multiplican.
Ejemplo
La matriz ampliada del sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.](/images/math/math-b4daf9b08947470816a091c908c8b878.png)
es:
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)](/images/math/math-9d6156e83361678f19df40db3ecf5638.png)
Si a la tercera y segunda fila le restamos la primera, obtenemos:
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)](/images/math/math-45eb9fde313d2a75f1b05cd42aac6c52.png)
Lo que acabamos de hacer es equivalente a restar a la tercera y segunda ecuación la primera.
Si ahora intercambiamos la segunda y tercera filas ( ecuaciones ), obtenemos la siguiente matriz triangular superior:
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)](/images/math/math-0730ab56aabea929252d49dbf9595acc.png)
que es la matriz ampliada del sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.](/images/math/math-eb6ec9bc0f3d4f3655e297c2d80271fe.png)
que es equivalente al inicial.
Solucionamos la tercera ocuacion para obtener
 :
:
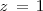
En la primera y segunda ecuación, sustituimos
 por la solucion de la tercera ecuación (
por la solucion de la tercera ecuación (
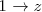 ), para obtener:
), para obtener:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.](/images/math/math-5c98a4989cffb856e694abe6316e1767.png)
La segunda ecuación es ahora una ecuación con una sola incognita,
 , que resolvemos para obtener
, que resolvemos para obtener
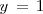 . Sustituimos, en la primera ecuación,
. Sustituimos, en la primera ecuación,
 por 1 (
por 1 (
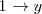 ). Esto nos da una ecuación en
). Esto nos da una ecuación en
 :
:

que al resolverla termina de darnos la solución del sistema de ecuaciones inicial:
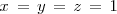
Método de la matriz inversa
Un sistema de ecuaciones lineales se puede escribir en forma matricial:

Si
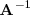 existe, es decir, si
existe, es decir, si
 es una matriz cuadrada de determinante no nulo, entonces podemos multiplicar toda
la igualdad anterior por la izquierda por
es una matriz cuadrada de determinante no nulo, entonces podemos multiplicar toda
la igualdad anterior por la izquierda por
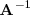 , para obtener:
, para obtener:
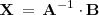
que es la solución del sistema de ecuaciones lineales de matriz de coeficientes
 y matriz de terminos independientes
y matriz de terminos independientes
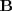 .
.
Regla de Cramer
Esta regla es un método de resolución de sistemas de ecuaciones lineales que se puede
utilizar cuando la matriz
 de coeficientes del sistema es cuadrada y de determinante no nulo. El que
de coeficientes del sistema es cuadrada y de determinante no nulo. El que
 sea cuadrada significa que el numero de incognitas y el numero de ecuaciones
coincide.
sea cuadrada significa que el numero de incognitas y el numero de ecuaciones
coincide.
Cuando el sistema de ecuaciones
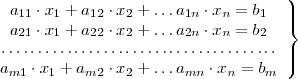
satisface las condiciones arriba mencionadas, su solución viene dada por:
![x_1 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
b_1 & a_{12} & \ldots & a_{1n}
\\
b_2 & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
b_m & a_{m2} & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}
, \qquad \qquad x_2 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & b_1 & \ldots & a_{1n}
\\
a_{21} & b_2 & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & b_m & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}, \qquad \qquad \ldots \ldots
x_1 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
b_1 & a_{12} & \ldots & a_{1n}
\\
b_2 & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
b_m & a_{m2} & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}
, \qquad \qquad x_2 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & b_1 & \ldots & a_{1n}
\\
a_{21} & b_2 & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & b_m & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}, \qquad \qquad \ldots \ldots](/images/math/math-57a8519773e4de96d9c3194f45f1c4b4.png)
![\ldots \ldots, \qquad \qquad x_n \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & b_1
\\
a_{21} & a_{22} & \ldots & b_2
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & b_m
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}
\qquad \qquad
\ldots \ldots, \qquad \qquad x_n \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & b_1
\\
a_{21} & a_{22} & \ldots & b_2
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & b_m
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}
\qquad \qquad](/images/math/math-569b5d8f60f1d2e21c769b195d3609c9.png)
En general
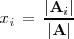
donde
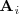 es la matriz que se obtiene sustituyendo la i-esima columna de
es la matriz que se obtiene sustituyendo la i-esima columna de
 por la matriz de los terminos independientes,
por la matriz de los terminos independientes,
 .
.
Ejemplo
Consideremos el sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, = \, 2
\\
x \, - \, y \, = \, 0
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, = \, 2
\\
x \, - \, y \, = \, 0
\end{array}
</pre>
<p>\right.](/images/math/math-9d7fa2a713677bcaf5cea62fe4a5126f.png)
En este sistema de ecuaciones lineales, la matriz
 de los coeficientes es una matriz cuadrada y
de los coeficientes es una matriz cuadrada y
![|\mathbf{A}| \, = \,
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & ~~1
\\
1 & -1
\end{array}
</pre>
<p>\right|
</p>
<pre>\, = \, -2 \neq 0
</pre>
<p>
|\mathbf{A}| \, = \,
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & ~~1
\\
1 & -1
\end{array}
</pre>
<p>\right|
</p>
<pre>\, = \, -2 \neq 0
</pre>
<p>](/images/math/math-657d3399a3d5de5fef04047646d22644.png) . Por lo tanto, podemos aplicar la regla de Cramer para resolverlo:
. Por lo tanto, podemos aplicar la regla de Cramer para resolverlo:
![x \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
2 & ~~1
\\
0 & -1
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|} \, = \, \frac{-2}{-2} \, = \, 1
\qquad \qquad y \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
1 & 2
\\
1 & 0
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}\, = \, \frac{-2}{-2} \, = \, 1
x \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
2 & ~~1
\\
0 & -1
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|} \, = \, \frac{-2}{-2} \, = \, 1
\qquad \qquad y \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
1 & 2
\\
1 & 0
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}\, = \, \frac{-2}{-2} \, = \, 1](/images/math/math-cc4c55b2e2b84ec9b768772cbfd55422.png)
estoy tragado de mi papito por que siempre me hace arroz con, mi papito se encuentra muy mal de salud, le dio varicela en la vagina





