Ángulo entre dos rectas
De Wikillerato
Ángulo entre una recta y un plano
El ángulo
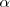 que forma una recta
que forma una recta
 cuyo vector director es
cuyo vector director es
 y un plano
y un plano
 cuyo ángulo normal es
cuyo ángulo normal es
 es complementario al ángulo que forman
es complementario al ángulo que forman
 y
y
 .
.
Por lo tanto, se tiene que
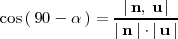
Podemos obtener un vector director de la recta
 multiplicando vectorialmente un vector perpendicular al plano:
multiplicando vectorialmente un vector perpendicular al plano:
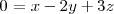
por un vector perpendicular del plano
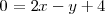
Un vector perpendicular al plano
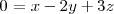
lo podemos obtener de los coeficientes de x, y, z en la ecuacion anterior:
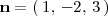
De la misma forma obtenemos un vector perpendicular al otro plano
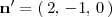
El producto vectorial de ambos vectores,
 y
y
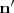 es
es
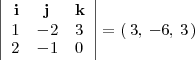
donde la segunda fila es
 y la tercera es
y la tercera es
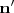 .
.



