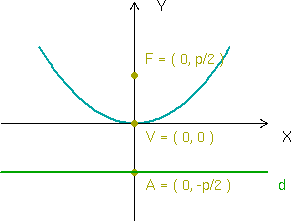Parábola
De Wikillerato
Definición
Llamamos lugar geometrico al conjunto de puntos que satisfacen una determinada propiedad.
Llamamos parábola al lugar geométrico de los puntos de un plano que equidistan
de un punto fijo
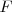 y de una recta fija
y de una recta fija
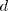 .
.
Veamos cuales son los elementos de la parábola:
1. El punto
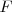 se denomina foco y la recta
se denomina foco y la recta
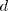 es la directriz de la parábola.
es la directriz de la parábola.
2. La recta que pasa por el foco y es perpendicular a la directriz se llama eje de la parábola. En la figura de arriba el eje de la parábola coincide con el eje [Unparseable or potentially dangerous latex formula. Error 3 ] .
3. El punto en el que el eje corta a la parábola recibe el nombre de vértice.
(
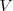 en la figura de arriba )
en la figura de arriba )
4. Se denomina parámetro,
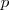 , a la distancia del foco a la directriz.
, a la distancia del foco a la directriz.
Ecuación
La condición:
"los puntos de la parábola equidistan de
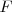 y de
y de
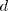 ."
."
se puede expresar matematicamente de la siguiente forma:
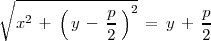
donde el miembro de la izquierda es la distancia de un punto
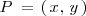 a
a
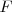 y el miembro de la derecha es la distancia de
y el miembro de la derecha es la distancia de
 a
a
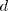 .
.
Elevando al cuadrado y agrupando terminos semejantes, obtenemos:
[Unparseable or potentially dangerous latex formula. Error 3 ]
Ejemplo
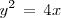
es la ecuación de una parábola cuyo eje es el eje
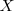 y cuya directriz es la recta de ecuación:
[Unparseable or potentially dangerous latex formula. Error 3 ]
. Su foco es el punto
y cuya directriz es la recta de ecuación:
[Unparseable or potentially dangerous latex formula. Error 3 ]
. Su foco es el punto
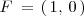 .
.