Desarrollo de un determinante
De Wikillerato
En esta sección se explica un procedimiento que nos permite calcular determinantes de cualquier orden, pero antes hemos de introducir los conceptos de menor complementario, adjunto y matriz adjunta.
Tabla de contenidos |
Menor complementario
Para una matriz cuadrada de orden
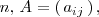 se llama menor complementario del elemento
se llama menor complementario del elemento
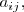 y lo representamos por
y lo representamos por
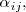 al determinante de la matriz cuadrada de orden
al determinante de la matriz cuadrada de orden
 que resulta de suprimir la fila
que resulta de suprimir la fila
 y la columna
y la columna
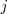 de la matriz
de la matriz

Ejemplo
Los menores complementarios de la matriz
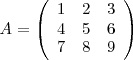
son
![\begin{array}{ccc}
\alpha_{11} =
\left|
</p>
<pre> \begin{array}[c]{cc}
5 & 6
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{12} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 6
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{13} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 5
\\
7 & 8
\end{array}
</pre>
<p>\right|
\\
& &
\\
\alpha_{21} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{22} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{23} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
7 & 8
\end{array}
</pre>
<p>\right|
\end{array}
\begin{array}{ccc}
\alpha_{11} =
\left|
</p>
<pre> \begin{array}[c]{cc}
5 & 6
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{12} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 6
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{13} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 5
\\
7 & 8
\end{array}
</pre>
<p>\right|
\\
& &
\\
\alpha_{21} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{22} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{23} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
7 & 8
\end{array}
</pre>
<p>\right|
\end{array}](/images/math/math-3783e29010f16c31576a73ebc6eb80c8.png)
![\begin{array}[c]{ccc}
\alpha_{31} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
5 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{32} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
4 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{33} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
4 & 5
\end{array}
</pre>
<p>\right|
\end{array}
\begin{array}[c]{ccc}
\alpha_{31} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
5 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{32} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
4 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{33} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
4 & 5
\end{array}
</pre>
<p>\right|
\end{array}](/images/math/math-03adb91ef28c3794b095ecb93b73fb77.png)
Matriz adjunta
Para una matriz cuadrada de orden
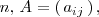 se llama adjunto del elemento
se llama adjunto del elemento
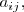 y lo representamos por
y lo representamos por
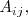 al producto
al producto
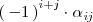 , es decir:
, es decir:

La matriz cuyos elementos son los adjuntos de los elementos de una matriz cuadrada
 se llama matriz adjunta de
se llama matriz adjunta de
 y se denota por
y se denota por
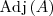
Ejemplo
Los adjuntos de la matriz
 del ejemplo anterior son:
del ejemplo anterior son:

La matriz adjunta de
 es
es
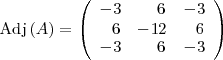
Desarrollo de un determinante
El determinante de una matriz cuadrada de orden  es igual a la suma de los productos de los elementos
de una línea o columna cualquiera por sus adjuntos respectivos. Simbolicamente:
es igual a la suma de los productos de los elementos
de una línea o columna cualquiera por sus adjuntos respectivos. Simbolicamente:
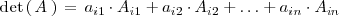
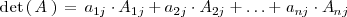
Ejercicios resueltos
Calcular un determinante 4x4
Desarrollo de un determinante utilizando sus propiedades generales



