Vector posición de un punto material y sistemas de referencia
De Wikillerato
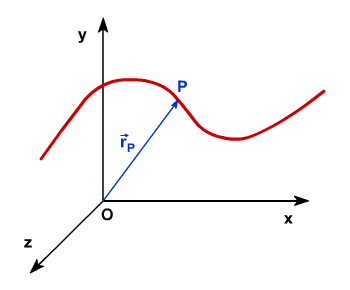
Al realizar el estudio analítico del movimiento podremos asimilar la posición del cuerpo a la de un punto, que denominamos punto material, que nos informa de esa posición en el espacio en cada instante.
La posición de ese punto P con relación al punto de referencia O queda definida por un segmento que con origen en O y extremo en P, indicando este extremo con una flecha, y que denominaremos vector posición del punto P.
Diremos que el punto se encuentra en la posición definida por el vector OP.
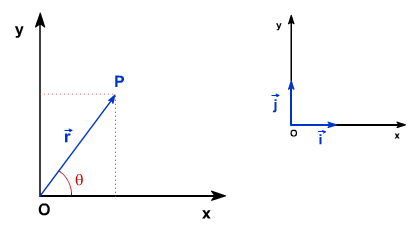
En el caso de que el móvil realice su movimiento contenido en un plano, caso de los movimientos parabólicos o circulares, si queremos determinar de un modo explícito la posición del cuerpo, necesitaremos definir un sistema de coordenadas cartesianas OXY. Si el cuerpo se encuentra en el punto P, carecemos de información suficiente para determinar su posición si sólo decimos que se encuentra a una distancia OP del origen de coordenadas, pues todos los puntos de una circunferencia de radio r = OP cumplen con esa condición. Habrá que conocer también el ángulo 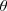 que forma OP con el eje OX. También podríamos conocer la posición del móvil si estamos informados de las coordenadas (x,y) del punto P.
que forma OP con el eje OX. También podríamos conocer la posición del móvil si estamos informados de las coordenadas (x,y) del punto P.
Vemos pues que, para definir la posición del móvil, necesitaremos conocer dos parámetros, bien sea el módulo de r y el ángulo 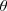 , y diremos que P viene definido por las coordenadas polares
, y diremos que P viene definido por las coordenadas polares 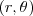 , o bien sea las coordenadas cartesianas de
, o bien sea las coordenadas cartesianas de 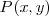 .
.
Entre las coordenadas 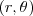 y
y 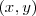 existe la relación:
existe la relación:
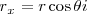
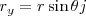
donde i y j son los vectores unitarios en las direcciones de los ejes oX y oY respectivamente. Se obtiene pues:
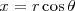
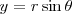
Si aplicamos el teorema fundamental de la trigonometría:
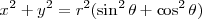
de donde
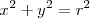
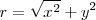
Apoyo analítico
Definimos como producto escalar de dos vectores al producto 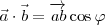 , siendo
, siendo 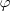 el ángulo formado por los dos vectores
el ángulo formado por los dos vectores
de este modo, dado que i y j son vectores unitarios (de módulo 1), encontramos
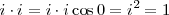
y también
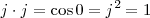
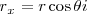
elevando al cuadrado ambas igualdades y sumando, encontramos
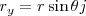
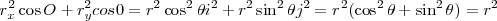
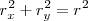
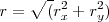
El módulo de un vector es igual a la raíz cuadrada de la suma de los cuadrados de sus componentes.
De igual modo podríamos obtener las componentes de un vector en un espacio tridimensional, definiendo el vector k como el vector unitario en la dirección del eje oZ, que sería perpendicular en O al plano definido por oXY, y 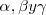 los ángulos que forma el vector r con los ejes oX, oY y oZ respectivamente.
los ángulos que forma el vector r con los ejes oX, oY y oZ respectivamente.
donde 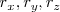 son las componentes del vector
son las componentes del vector 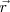 según las direcciones de los ejes de coordenadas. Es decir:
según las direcciones de los ejes de coordenadas. Es decir: 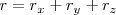 o bien
o bien 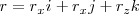
Como se puede ver,
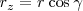 puesto que
puesto que 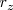 es la proyección de
es la proyección de 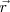 sobre el eje oZ, que determina la coordenada
sobre el eje oZ, que determina la coordenada 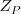 . El segmento OM es la proyección de
. El segmento OM es la proyección de 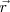 sobre el plano definido por OXY, por lo cual
sobre el plano definido por OXY, por lo cual
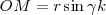
Si proyectamos OM sobre los ejes OX y OY, obtenemos:
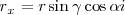
elevando al cuadrado ambas ecuaciones y sumando, tenemos
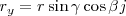
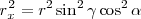
teniendo en cuenta que 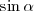 es igual a
es igual a 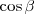
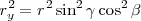
obtenemos:
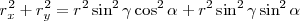
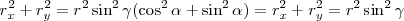
recuperando 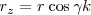 , elevándola al cuadrado y sumada a la ecuación precedente
, elevándola al cuadrado y sumada a la ecuación precedente
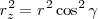
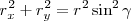
nos queda
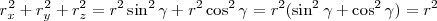 con lo cual:
con lo cual:
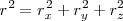
el cuadrado de un vector es igual a la suma de los cuadrados de sus componentes.
Por otra parte: 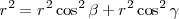 si simplificamos queda:
si simplificamos queda:
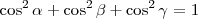
De un modo general, la suma de los cuadrados de los cosenos directores de un vector es igual a 1.