Algunos problemas con triángulos
De Wikillerato
Estos problemas son ejemplos de aplicación de las propiedades estudiadas.
Tabla de contenidos[ocultar] |
Problema de Napoleón
Este problema atribuido al emperador francés es realmente otra propiedad de los triángulos, aunque se la conoce con el nombre de problema: “Si en un triángulo arbitrario  se construye un equilátero con un lado coincidente con cada lado, los puntos notables de estos triángulos determinan otro equilátero”.
se construye un equilátero con un lado coincidente con cada lado, los puntos notables de estos triángulos determinan otro equilátero”.
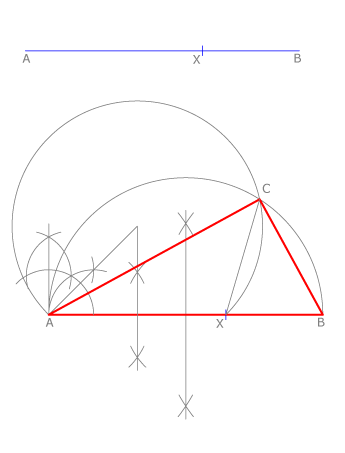
Problema I
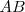 es la hipotenusa de un triángulo.
es la hipotenusa de un triángulo. 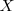 es el punto por el que pasa la bisectriz de ángulo en
es el punto por el que pasa la bisectriz de ángulo en  . Construir el triángulo
. Construir el triángulo  .
.
El triángulo buscado es rectángulo, siendo 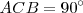 . Si dibujamos el arco capaz de
. Si dibujamos el arco capaz de 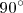 para
para 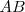 y el de
y el de 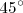 para
para 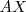 el problema está resuelto. El punto
el problema está resuelto. El punto  es la intersección de los dos arcos capaces. Hay otra solución simétrica a
es la intersección de los dos arcos capaces. Hay otra solución simétrica a  respecto de
respecto de 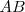 .
.
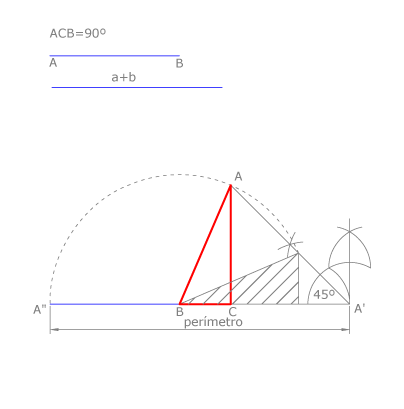
Problema II
En un triángulo el ángulo 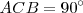 , el lado
, el lado 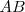 y la suma de los lados
y la suma de los lados  son segmentos dados. Construir el triángulo
son segmentos dados. Construir el triángulo  .
.
Dibujamos el perímetro del triángulo que es el segmento 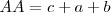 , pues
, pues 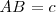 . Señalamos el punto
. Señalamos el punto 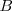 , pues
, pues 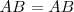 . El punto
. El punto  estará en la circunferencia de centro
estará en la circunferencia de centro 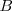 y radio
y radio 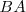 .
.
Dibujamos en 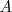 el ángulo de
el ángulo de 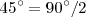 . El lado del ángulo corta al arco de circunferencia en las dos posiciones del punto
. El lado del ángulo corta al arco de circunferencia en las dos posiciones del punto  . Dibujamos
. Dibujamos  . El otro resultado, rayado, es el mismo triángulo colocado con los catetos en distinta dirección.
. El otro resultado, rayado, es el mismo triángulo colocado con los catetos en distinta dirección.
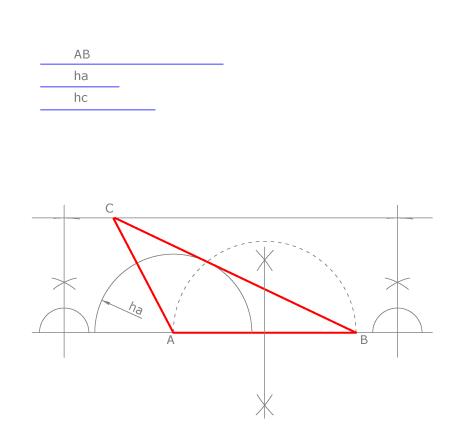
Problema III
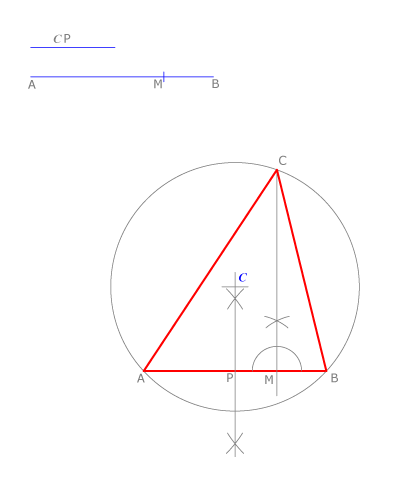
Conocemos el lado 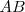 de un triángulo y sus alturas
de un triángulo y sus alturas 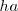 y
y 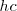 . Construir el triángulo
. Construir el triángulo  .
Dibujamos el lado
.
Dibujamos el lado 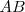 y una recta paralela a
y una recta paralela a 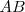 a la distancia
a la distancia 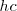 .
Trazamos un arco con radio
.
Trazamos un arco con radio 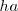 y centro en
y centro en  y la tangente desde
y la tangente desde 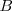 a dicho arco. El punto
a dicho arco. El punto  será la intersección de la paralela con la tangente.
será la intersección de la paralela con la tangente.
Hay otra solución simétrica a  respecto de
respecto de 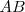 .
.
Problema IV
Conocemos el lado 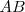 de un triángulo, un vértice
de un triángulo, un vértice 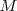 de su órtico y sabemos que el circuncentro
de su órtico y sabemos que el circuncentro  dista una magnitud dada,
dista una magnitud dada, 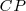 , de
, de 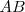 . Construir el triángulo.
. Construir el triángulo.
Hallamos la mediatriz de 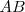 y situamos el circuncentro sobre ella. Dibujamos la circunferencia circunscrita, donde estará el vértice
y situamos el circuncentro sobre ella. Dibujamos la circunferencia circunscrita, donde estará el vértice  buscado. Como
buscado. Como 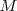 es un vértice del órtico, es el pie de la altura sobre
es un vértice del órtico, es el pie de la altura sobre 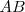 . Trazamos una perpendicular por
. Trazamos una perpendicular por 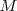 y hallamos
y hallamos  en su intersección con la circunscrita. Existe otra solución simétrica respecto de
en su intersección con la circunscrita. Existe otra solución simétrica respecto de 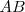 .
.
Problema V
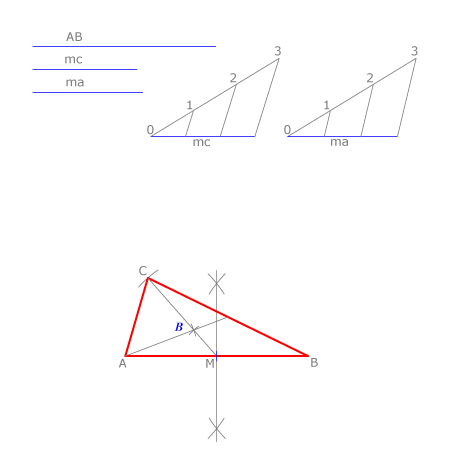
Conocemos el lado 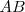 de un triángulo y sus medianas
de un triángulo y sus medianas 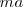 y
y 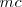 . Construir el triángulo.
. Construir el triángulo.
Trazamos la mediatriz de 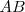 para hallar su punto medio
para hallar su punto medio 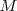 .
.
Dividimos en tres partes iguales cada mediana. Con centro en  y radio
y radio 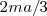 trazamos un arco. Con centro en
trazamos un arco. Con centro en 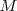 y radio
y radio 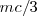 trazamos otro arco que cortará al anterior en el baricentro. Una vez situadas las medianas, llevamos la magnitud
trazamos otro arco que cortará al anterior en el baricentro. Una vez situadas las medianas, llevamos la magnitud 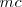 desde
desde 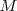 , asì hallamos
, asì hallamos  y trazamos el triángulo
y trazamos el triángulo  .
.
Problema VI
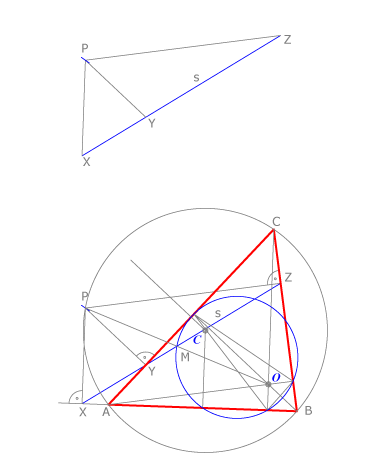
Conocemos un punto P de la circunferencia circunscrita al triángulo ABC, su recta de Simson s y las perpendiculares desde P la los lados del triángulo. Dibujar ABC y su circunferencia de Feuerbach. Comprobar que si O es el ortocentro, el punto medio de PO está sobre s y sobre dicha circunferencia. Trazamos por X, Y y Z las perpendiculares a PX, PY y PZ respectivamente, que son las tres rectas que determinan el triángulo ABC. Hallamos su ortocentro O y su circunferencia de Feuerbach y comprobamos la posición del punto M como nos indica el enunciado. Podemos también comprobar que P está en la circunscrita de ABC.
Problema VII
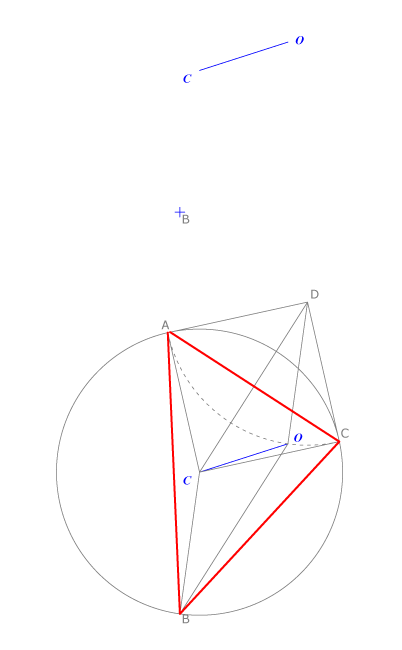
Conocemos el segmento CO determinado por el circuncentro y el ortocentro de un triángulo ABC y su vértice B. Construir el triángulo. Trazamos la circunferencia circunscrita con centro en el circuncentro C y radio CB. Sabemos que el vector CO es la suma de los vectores CA+CB+CC, siendo C el circuncentro. Realizamos la operación inversa hallando CD; igual y paralelo a BO, tal que CB +CD=CO. Por D trazamos un arco de radio igual al radio de la circunscrita ya que CA=CB=CC son radios de dicha circunferencia. Sus intersecciones con la circunscrita son los puntos A y C vértices de ABC. Comprobamos que el vector CD=CA+CC y por lo tanto CO=CA+CB+CC.
Problema VIII
Conocemos el circuncentro, un vértice A la recta na que contiene a la mediana que pasa por A y la mediatriz ma. Construir el triángulo ABC. Dibujamos la circunscrita con centro en C y radio CA. Por el punto de intersección de na con ma trazamos la perpendicular a ma, obteniendo los vértices B y C de la solución.
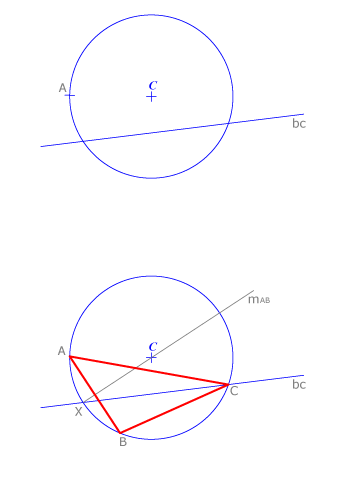
Problema IX
Conocemos la circunferencia circunscrita a un triángulo ABC, el vértice A y la bisectriz bC . Construir el triángulo ABC. La bisectriz bC se cortará con la mediatriz del lado AB opuesto al ángulo en C en un punto X de la circunscrita. La recta XC es la mediatriz de AB, mAB . El vértice B es simétrico de A respecto a dicha mediatriz. Por otra parte la bisectriz bC corta a la circunscrita en el vértice C.
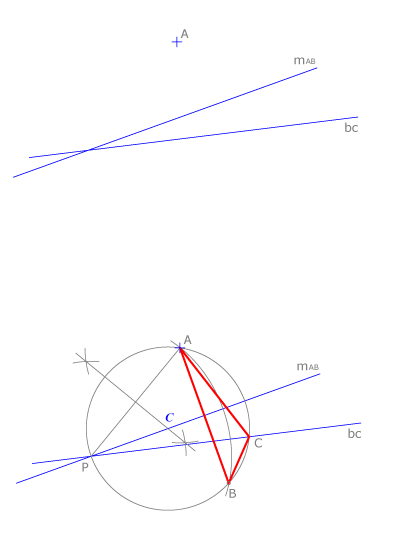
Problema X
Conocemos la mediatriz mAB , la bisectriz bC y un punto A del triángulo ABC. Construir dicho triángulo. La intersección de la mediatriz y la bisectriz dadas es un punto P que pertenece a la circunscrita de ABC. Trazamos la mediatriz de AP y hallamos el centro de dicha circunscrita, que dibujamos. El punto B es el simétrico de A respecto de mAB y el punto C la intersección de bC con la circunscrita. Dibujamos ABC.
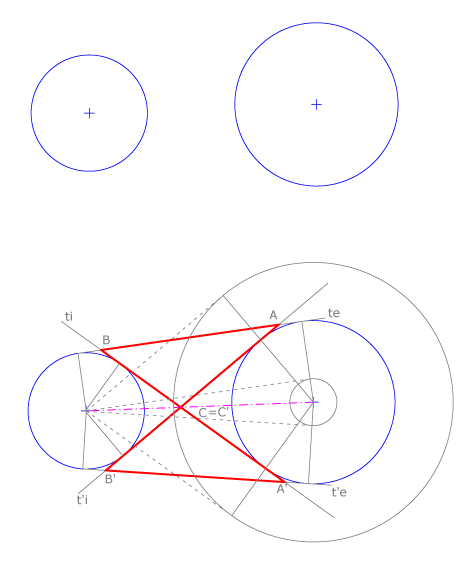
Problema XI
Conocemos dos circunferencias exinscritas a un triángulo ABC. Construir el triángulo. Trazamos las rectas tangentes comunes interiores y exteriores a las circunferencias dadas. Los triángulos solución, simétricos respecto de la recta que une los centros de las circunferencias, son ABC y A’B’C’.
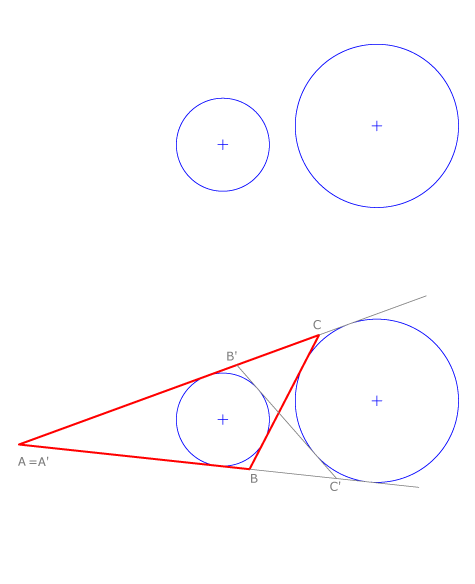
Problema XII
Conocemos dos circunferencias, la menor inscrita y la mayor exinscrita a un triángulo ABC. Construir el triángulo. Trazamos las rectas tangentes comunes interiores y exteriores a las circunferencias dadas. Los triángulos solución, simétricos respecto de la recta que une los centros de las circunferencias, son ABC y A’B’C’.
Problema XIII
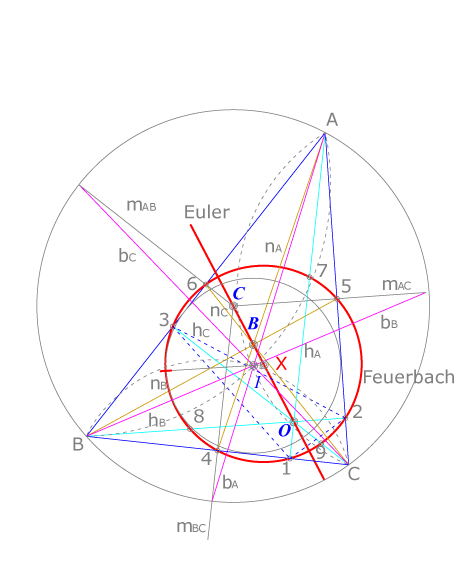
Dado un triángulo ABC, construir sus circunferencias inscrita, circunscrita y de Feuerbach, sus puntos y rectas notables y su recta de Euler. En la figura también se ha señalado el punto de tangencia entre la circunferencia inscrita y la de Feuerbach.