Los espectros atómicos y las transiciones electrónicas

De Wikillerato

Antecedentes históricos: Espectroscopia

El hombre ha tenido a lo largo de su historia contacto con uno de los fenómenos naturales más bellos que se manifiesta en un día de Sol, pero con un algunas nubes que descargan lluvia, un maravilloso “arco iris” se puede visualizar en el cielo en el lado opuesto de Sol. Aunque debería estar claro que el fenómeno estaba ligado a la presencia conjunta de luz y agua, no se comenzó a tener una idea científica clara del fenómeno hasta que en el año 1666 el gran científico Isaac Newton (1643-1726) pudo “descomponer” con un prisma de vidrio la luz blanca del Sol en los “siete” colores carasterístico de su “alma” o espectro y recomponer de nuevo el rayo de luz blanca a partir de sus colores con un segundo prisma. Newton había descubierto la dispersión de la luz por la materia, un aspecto que resultó esencial para la comprensión de la naturaleza física de la luz. Este experimento está descrito en su tratado de Óptica (Opticks en latín) publicado en 1704.

Hubo que esperar ciento cincuenta años hasta que en 1814, el físico alemán Joseph Von Fraunhofer (1787-1826) observara unas lineas o rayas oscuras (más de 600) en el espectro de la luz solar, [una observación anterior de lineas oscuras en 1802, fue realizada por el físico y químico británico William Wollaston (1766-1828)] que fueron interpretadas en 1859 por los también físicos alemanes Robert-Wilhelm Busen (1811-1899) y Gustav-Robert Kirchhoff (1824-1887) como absorciones de la luz por los átomos (en este particular caso por los gases situados en la atmósfera solar).

Poco después un número de científicos observaron rayas brillantes muy estrechas y bien definidas en el espectro de la luz emitidas por llamas, arcos voltaicos y chispas. Había nacido la espectroscopia, el espectroscopio, el aparato que sirve para separar (analizar) los distintos componentes de una emisión lumínica en función de su longitud de onda (o frecuencia), que con una configuración experimental basada esencialmente en aquella introducida por Newton en el siglo XVII, se convertiría así en unos de los instrumentos esenciales de la física moderna.

Utilizando este nuevo instrumento los primeros espectroscopistas, pudieron determinar que los elementos y compuestos químicos emiten tres tipos de espectro general. El espectro de emisión continuo, emitido principalmente por sólidos o líquidos incandescentes, que no muestran ningún tipo de linea o raya brillante u oscura cuando la luz emitida por los mismos es observada en los espectroscopios de más alto poder de resolución. Si por otra parte aparecen rayas oscuras en un espectro de emisión continuo tenemos entonces un espectro de absorción, denominando a esas rayas o lineas de absorción. Por otra parte los espectros de emisión bandas, que consisten en grupos de líneas brillantes que parecen ser continuas en espectroscopias de bajo poder de resolución. Este tipo de espectro es emitido cuando pequeñas piezas de material de un compuestoson calentados en una llama o con un electrodo. Por último, los espectros de emisión de lineas que se originan en la luz emitida por fuentes que contienen únicamente elementos químicos puros (e.g. un gas luminoso rarificado excitado en un tubo de descarga). Así, las rayas y bandas observados en estos resultan ser características de los elementos químicos individuales y de los compuestos químicos respectivamente cuando son excitados en determinadas condiciones. De hecho, los espectros de cada elemento o compuesto son como una “huella dactilar” que identifica a los mismos, son por ello llamados espectros característicos.

La existencia de los espectros de emisión lineas y bandas fue un resultado experimental que la física clásica no podía explicar, esta era solo capaz de explicar los espectros de emisión continuos (aunque no su forma detallada como ocurrió al estudiar la radiación de cuerpo negro [[1]], pero no podía explicar la existencia y el origen de esas rayas discretas. Explicar el espectro de emisión de líneas del elemento más simple, el hidrógeno se convertiría en el trabajo de los físicos durante el primer cuarto de siglo XX, y necesito de los trabajos de Planck, Einstein y Bohr, y para la explicación de las líneas y bandas más finas del espectro se requirió finalmente del desarrollo de la teoría cuántica.

Un espectro atómico es la radiación característica emitida por los átomos de un elemento individual en una llama o en un gas excitado por una descarga eléctrica. Cuando esa radiación es observada a través de un espectroscopio, la radiación aparece como un conjunto de líneas estrechas o rayas discretas cada una de un color particular o longitud de onda. Las posiciones e intensidades de cada una de las rayas son características de cada elemento. La longitud de onda de estas líneas se puede determinar con gran precisión. El primer avance significativo en la compresión de estas rayas, se produjo en 1885 cuando un profesor de matemáticas de escuela suizo llamado Johann J. Balmer (1825-1898) encontró que las rayas en la región del espectro visible del espectro de hidrógeno , el cual contiene cuatro rayas una roja, otra azul y dos violeta, con una longitud de onda de 656 nm 486 nm 410 nm y 434 nm respectivamente producido por el análisis espectroscópico de la luz emitido por átomos de hidrógeno , conocidas por ello ahora como serie Balmer podrían ser representadas y obtenidas por aplicación de la fórmula empírica:

[Unparseable or potentially dangerous latex formula. Error 3 ] 

con la la longitud de onda [Unparseable or potentially dangerous latex formula. Error 3 ] dada en nanómetros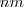

donde 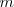es un número entero, el cual puede tomar los valores 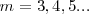. Por ejemplo para ver como la fórmula de Balmer funciona, se la la longitud de onda de la línea roja llamada 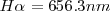del espectro del hidrógeno, si entonces introducimos 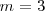en la fórmula de Balmer tenemos que la misma nos dá la longitud de onda 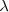de esta raya 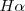. La formula como se puede comprobar dá cada una de las longitudes de onda menores a medida que 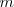aumenta hasta .

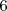El propio Balmer en vida pudo comprobar con gran satisfacción que una predicción realizada usando esta formula, predijo el valor de la longitud para cuando 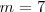se confirmó experimentalmente (con ello cumplió el sueño más preciado de todo teórico, la confirmación experimental de sus predicciones teóricas) por Ångström había observado una línea con una longitud de onda de 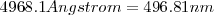Además, otros dos colegas de la ciudad en la que residia Balmer H. W. Vogel y Huggins fueron capaces de confirmar la existencia de otras líneas de la serie de Balmer a partir del espectro de hidrógeno observado al analizar la luz de estrellas blancas, todo un logro.

Balmer sugirío además que esta fórmula podría podría ser un caso especial de una expresión más general aplicable a los espectros de otros elementos químicos. El físico sueco J. R. Rydberg (1854-1919) y el físico suizo W. Ritz (1878-1909) derivaron independientemente la así llamada formula Rydberg-Ritz:

 [Unparseable or potentially dangerous latex formula. Error 3 ]  

donde el inverso de la longitud de onda es el llamado número de onda ; 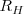es la constante Rydberg para el hidrógeno, 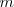un número entero con [Unparseable or potentially dangerous latex formula. Error 3 ]que designa la serie y otro número entero [Unparseable or potentially dangerous latex formula. Error 3 ]que da el termino de la serie. Esta expresión empírica son útiles en predecir en lineas espectrales del hidrógeno más allá del espectro visible. En términos mñas generales 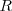, es la constante de Rydberg, es la misma para toda una serie de lineas espectrales del mismo elemento y varia solo ligeramente de elemento, de una manera regular , de un elemento a otro. Para el hidrógeno el valor de 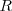es 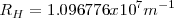. Para elemento pesados 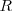se aproxima a un valor .

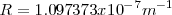Cuando introducimos 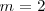en la fórmula se obtiene otra expresión de la fórmula de Balmer:

 [Unparseable or potentially dangerous latex formula. Error 3 ] 

Principio de combinación de Ritz

Los primeros espectroscopistas fueron capaces de encontrar otras regularidades en los espectros atómicos. En 1908 W. Ritz (1878-1909) enuncio un principio de espectroscopia llamado principio de combinación de Ritz:

Para un átomo dado, es posible encontrar una sucesión discontinua de frecuencias, llamadas términos espectrales, de manera que la frecuencia de cualquier raya espectral de dicho átomo se obtiene con la diferencia entre dos de estos terminos. En otras palabras, los números de onda 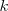de muchas de las rayas espectrales de un elemento son iguales a diferencias o sumas, del número de ondas de otros pares de onda. En términos matemáticos precisos, tenemos por ejemplo que cierto elemento tiene las siguientes rayas en su especro atómico 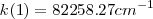; 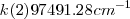y 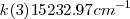, tenemos así que la diferencia entre el número de onda estas dos rayas 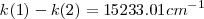un valor que está muy próximo a .

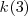Posteriormente se describio un principio más general, por el cual el número de onda de cualquier raya emitida por un átomo puede expresarse como diferencia 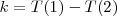de dos términos espectrales 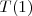y 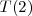. Cada átomo está caracterizado por un conjunto de terminos (expresado como conjunto números de onda) conocido como sistema de términos del átomo. Por ejemplo supongamos que tres rayas espectrales están asociadas como sigue con tres términos:

[Unparseable or potentially dangerous latex formula. Error 3 ] [Unparseable or potentially dangerous latex formula. Error 3 ] [Unparseable or potentially dangerous latex formula. Error 3 ]

tenemos entonces,

[Unparseable or potentially dangerous latex formula. Error 3 ]

Que es un ejemplo del principio de combinación de Ritz

La explicación de estas regularidades espectroscópicas se encontraría en el modelo de Bohr, que interpretaria un término espectral como correspondiente a un nivel energético del átomo y el sistema de términos se interpreta por consiguiente como manifestación de un conjunto de niveles característicosdel átomo en cuestión.

Así, la búsqueda de un modelo atómico que diera cuenta las peculiaridades experimentales observadas en los espectros atómicos fue una de las grandes tareas que abordaron los físicos en la primera década del siglo XX.

Bibliografia

Eyvind. H. Wichmann. Física cuántica. Berkeley Physics Course. Vol 4. Editorial Reverté, S.A. 1991. Un excelente introducción a la física cuántica y a los espectro atómicos.

Enlaces externos