Elipse
De Wikillerato
Tabla de contenidos |
Definición
Llamamos lugar geometrico al conjunto de puntos que satisfacen una determinada propiedad.
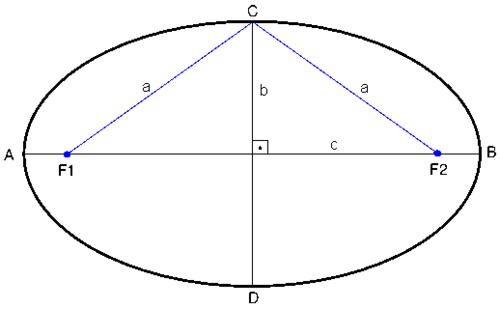
Llamamos elipse al lugar geométrico de los puntos de un plano cuya suma de
distancias a dos puntos fijos del plano es constante este valor es 2a,
 y
y
 , es constante. Veamos sus elementos en los siguiente dibujos:
, es constante. Veamos sus elementos en los siguiente dibujos:
Los puntos fijos
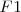 y
y
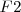 se denominan focos, siendo el eje focal la recta que pasa por
ellos.
se denominan focos, siendo el eje focal la recta que pasa por
ellos.
Se llama eje secundario a la mediatriz del segmento
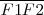 . El punto medio de dicho segmento es el centro de la elipse.
. El punto medio de dicho segmento es el centro de la elipse.
Los dos ejes de la elipse cortan a ésta en cuatro puntos,
 ,
,
 ,
,
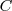 y
y
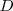 que reciben el nombre de vértices .
que reciben el nombre de vértices .
La distancia focal es la que hay entre los focos y se expresa por
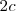 . La mitad de esta distancia,
. La mitad de esta distancia,
 , es la semidistancia focal.
, es la semidistancia focal.
Para cualquier punto
 de la elipse, se verifica que
de la elipse, se verifica que
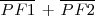 es constante. Llamamos a esta constante
es constante. Llamamos a esta constante
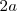 .
.
El segmento
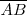 es el eje mayor de la elipse. La longitud del eje mayor es
es el eje mayor de la elipse. La longitud del eje mayor es
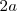 . La mitad de esta distancia,
. La mitad de esta distancia,
 , se denomina semieje mayor.
, se denomina semieje mayor.
El segmento
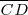 es el eje menor de la elipse y su longitud se expresa por
es el eje menor de la elipse y su longitud se expresa por
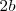 . La mitad de esta distancia,
. La mitad de esta distancia,
 , es el semieje menor.
, es el semieje menor.
Si aplicamos el teorema de Pitagoras al triangulo rectangulo que forman los puntos
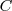 ,
,
 y el centro de la elipse, concluimos que en cualquier elipse se cumple la relación:
y el centro de la elipse, concluimos que en cualquier elipse se cumple la relación:
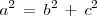
La excentricidad de una elipse es su grado de achatamiento y su valor está determinado por la expresión:
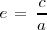
Cuanto mayor es la excentricidad mas achatada es la elipse.
En una elipse
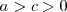 y por lo tanto la excentricidad es positiva y menor que uno.
y por lo tanto la excentricidad es positiva y menor que uno.
¿Existira alguna relación entre la excentricidad de una elipse y la excentricidad de una persona?
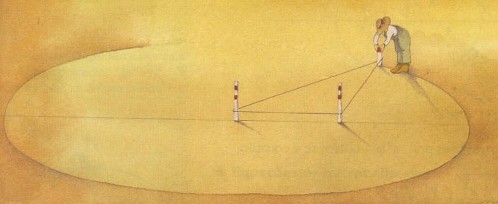
En la imagen de abajo vemos a un jardinero que esta dibujando una elipse en un jardin para poner en él sus rosales. Ha puesto dos estacas en el suelo separadas una cierta distancia y esta utilizando una cuerda con sus extremos unidos. El jardinero tensa la cuerda con las dos estacas y una vara que sujeta con la mano y dibuja la elipse creando un surco con la vara mientras se asegura de que la cuerda siempre forma un triangulo:
Ecuación
Supongamos que el origen de cordenadas esta en el centro de la elipse y que el eje focal
coincide con el eje
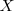 , entonces los focos son:
, entonces los focos son:
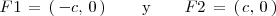
La condición de que la suma de la distancias de un punto cualquiera de la elipse,
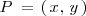 , a los focos es
, a los focos es
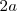 se puede expresar matematicamente de la siguiente forma:
se puede expresar matematicamente de la siguiente forma:
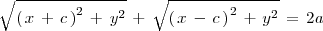
Igualdad que es equivalente a esta otra:
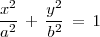
que constituye la ecuación reducida de la elipse.
Ejemplo
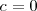 y, por tanto, la excentricidad de una circunferencia es 0.
y, por tanto, la excentricidad de una circunferencia es 0.
Referencias
- Cónicas: Ecuaciones de la circunferencia y la elipse, Pilar Ferrero Casado. Matemáticas: ESO, Bachillerato y Selectividad.
- Cónicas: Webs dinámicas con GeoGebra, Manuel Sada Allo