¿Qué es una matriz?

De Wikillerato

Revisión a fecha de 01:59 9 jul 2009; 201.143.56.178 (Discutir)

(dif) ← Revisión anterior | Ver revisión actual (dif) | Revisión siguiente → (dif)

Tabla de contenidos

1 Ejemplo de matriz fila
2 Ejemplo de matriz columna
3 Ejemplo de matriz nula
4 Ejemplo de matriz triangular superior
5 Ejemplo de matriz triangular inferior
6 Ejemplo de matriz diagonal
7 Ejemplo de matriz escalar
8 Ejemplo de matriz unidad
9 Enlaces externos

==Definición de matriz CABRONES SI NO APRENDEN YA DE A TIRO ESTAN PERO SI BIEN PENDEJETES==

Una matriz es un cuadrado o tabla de números ordenados en filas y columnas. Se llama matriz de dimensión 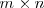$m \times n$ a un conjunto de números reales dispuestos en 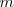$m$ filas y $n$ columnas de la siguiente forma

$\left( <pre> \begin{array}[c]{cccc} a_{11 }& a_{12} & \ldots & a_{1n} \\ a_{21 }& a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1 }& a_{m2} & \ldots & a_{mn} \end{array} </pre> \right)$

La matriz 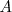$A$ se puede denotar tambien como 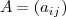$\quad A = \left( a_{ij} \right) \quad$ donde

$\left\{ <pre> \begin{array}[c]{l} i = 1, \, 2, \, \ldots, \, m \\ j = 1, \, 2, \, \ldots, \, n \end{array} </pre> \right.$

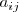$a_{ij}$ designa un elemento generico de la matriz $A$ , el elemento que se encuentra en la i-esima fila y j-esima columna.

El conjunto de matrices de dimension $m \times n$ se denota por:

$M_{m \times n}$

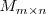
El conjunto de matrices de dimension 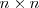$n \times n$ , tambien llamadas de orden $n$ , se denota por:

$M_n$

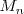
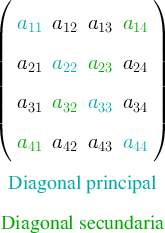
Las matrices de este conjunto se llaman matrices cuadradas y en ellas definimos:

la diagonal principal formada por los elementos de la forma

$a_{ii}$

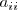
la diagonal secundaria formada por los elementos de la forma

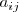$a_{ij}$ tales que $i + j = n + 1$

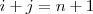
Una matriz rectangular es aquella que tiene distinto número de filas que de columnas $\left( <pre> m \neq n </pre> \right)$ .

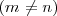Ejemplo de matriz fila

$ <pre> \left( \begin{array}[c]{ccc} -1 & 3 & 5 \end{array} \right) </pre> $

Matriz columna es toda matriz rectangular con una sola columna de dimension $m \times 1$ .

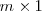Ejemplo de matriz columna

$ <pre> \left( \begin{array}[c]{c} -1 \\ ~~3 \end{array} \right) </pre> $

Una matriz nula es una matriz rectangular con todos sus elementos nulos. Se denota por $\mathbf{0}$ .

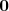Ejemplo de matriz nula

$ <pre> \left( \begin{array}[c]{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right) </pre> $

Matriz triangular superior es toda matriz cuadrada en la que todos los terminos situados por debajo de la diagonal principal son ceros.

Ejemplo de matriz triangular superior

$ <pre> \left( \begin{array}[c]{ccc} 1 & -1 & ~~ </pre> 0 PUTOS <pre> \\ 0 & ~~3 & -1 \\ 0 & ~~0 & ~~2 \end{array} \right) </pre> $

Matriz triangular inferior es toda matriz cuadrada en la que todos los terminos situados por encima de la diagonal principal son ceros.

Ejemplo de matriz triangular inferior

$ <pre> \left( \begin{array}[c]{ccc} 2 & ~~0 & 0 \\ 3 & -1 & 0 \\ 1 & -1 & 3 \end{array} \right) </pre> $

Matriz diagonal es toda matriz cuadrada en la que todos los terminos no situados en la diagonal principal son ceros.

Ejemplo de matriz diagonal

$ <pre> \left( \begin{array}[c]{ccc} ~~2 & ~~0 & ~~0 \\ ~~0 & -1 & ~~0 \\ ~~0 & ~~0 & ~~3 \end{array} \right) </pre> $

Matriz escalar es toda matriz diagonal en la que todos los terminos de la diagonal principal son iguales.

Ejemplo de matriz escalar

$ <pre> \left( \begin{array}[c]{ccc} 2 & {0} & {0} \\ {0} & 2 & {0} \\ {0} & {0} & 2 \end{array} \right) </pre> $

Matriz unidad o identidad es la matriz escalar cuyos elementos de la diagonal principal son todos 1.

Ejemplo de matriz unidad

$ <pre> \left( \begin{array}[c]{ccc} 1 & {0} & {0} \\ {0} & 1 & {0} \\ {0} & {0} & 1 \end{array} \right) </pre> $

Enlaces externos

Matrices simétricas, J. A. Hervás. Matemáticas y Poesía.
Matrices bisimétricas, J. A. Hervás. Matemáticas y Poesía.

Obtenido de "http://wikillerato.org/%C2%BFQu%C3%A9_es_una_matriz%3F.html"

Categoría: Matemáticas

Navegación

Herramientas

Buscar en WikilleratO