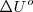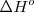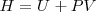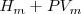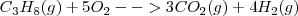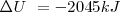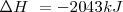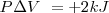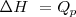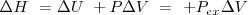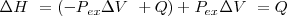Reacciones químicas a presión constante: Entalpía
De Wikillerato
Entalpía
Entalpía de griego θαλπω (calentar), una función introducida en termodinámica por el científico Heike Kammerlingh Onnes (1853-1926), es definida como:
Esto es, la entalpía 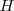 difiere de la
difiere de la 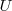 por la adición del producto de la presión
por la adición del producto de la presión 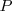 , y el volumen
, y el volumen 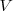 del sistema. Esta expresión se aplica a cualquier producto y a cualquier substancia.
del sistema. Esta expresión se aplica a cualquier producto y a cualquier substancia.
Las unidades del SI para la entalpía, 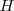 son los julios, J. En química generalmente se trabaja con cantidades molares y entonces las unidades de
son los julios, J. En química generalmente se trabaja con cantidades molares y entonces las unidades de 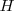 y
y 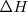 son
son 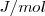 o
o 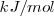 .
.
Un cambio en la entalpía 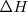 (la sola cantidad que se puede medir en términos prácticos) se origina por un cambio en la energía interna
(la sola cantidad que se puede medir en términos prácticos) se origina por un cambio en la energía interna 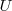 y un cambio en el producto
y un cambio en el producto 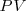 :
:
Donde 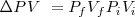 Si el cambio tiene lugar a presión constante P, el segundo término de la derecha se simplifica a :
Si el cambio tiene lugar a presión constante P, el segundo término de la derecha se simplifica a :
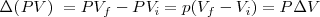 y se puede escribir:
y se puede escribir:
A presión constante: 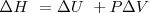
La entalpía es una propiedad extensiva. La entalpía molar 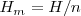 de una sustancia es una propiedad intensiva. Difiere de la energía interna molar por una cantidad proporcional al volumen,
de una sustancia es una propiedad intensiva. Difiere de la energía interna molar por una cantidad proporcional al volumen, 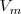 de la subtancia:
de la subtancia:
Esta relación es válida para cualquier sustancia.
Muchas reacciones químicas transcurren a presión constante (generalmente la atmosférica) donde el volumen del sistema puede cambiar. Para ver porque es necesario introducir una nueva función de estado (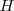 en esta cirsunstancia termodinámica consideremos los siguientes ejemplos:
en esta cirsunstancia termodinámica consideremos los siguientes ejemplos:
La descomposición térmica de 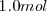 de
de 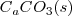 a
a 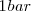 de presión resulta en un incremento del volumen en 89 L (litros) a 800 ºC debido al
de presión resulta en un incremento del volumen en 89 L (litros) a 800 ºC debido al 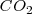 . Para crear este gran volumen que ocupa el dióxido de carbono, la atmosfera que rodea debe ser empujada por el
. Para crear este gran volumen que ocupa el dióxido de carbono, la atmosfera que rodea debe ser empujada por el 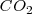 . Esto es el sistema tiene que realizar trabajo de expansión. Por lo tanto aunque cierta cantidad de calor es suministrada para llevar a cabo la descomposición endotérmica, el incremento en la energía interna del sistema no es igual al calor transferido al sistema, debido a que parte de esta energía ha sido utilizada para hacer trabajo de expansión. En otras palabras debido a que el volumen se ha incrementado, algo del calor suministrado ha salido del sistema de vuelta al ambiente como trabajo
. Esto es el sistema tiene que realizar trabajo de expansión. Por lo tanto aunque cierta cantidad de calor es suministrada para llevar a cabo la descomposición endotérmica, el incremento en la energía interna del sistema no es igual al calor transferido al sistema, debido a que parte de esta energía ha sido utilizada para hacer trabajo de expansión. En otras palabras debido a que el volumen se ha incrementado, algo del calor suministrado ha salido del sistema de vuelta al ambiente como trabajo 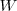 .
.
Otros ejemplos:
La combustión del propano 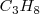 puede realizarse a presión constante, liberándose 2043 kJ de energía calorífica (calor). Por otra parte si esa reacción se lleva a cabo volumen constante (el trabajo de expansión no es posible por lo que toda la energía es liberada en forma de calor la energía liberda como calor es de -2045 kJ. La diferencia de 2 kJ, debido a que a presión constante, una pequeña cantidad de trabajo de expansión es hecho contra la atmosfera ya que 6 mol de reactivos gaseosos son convertidos en 7 mol de productos gaseosos
puede realizarse a presión constante, liberándose 2043 kJ de energía calorífica (calor). Por otra parte si esa reacción se lleva a cabo volumen constante (el trabajo de expansión no es posible por lo que toda la energía es liberada en forma de calor la energía liberda como calor es de -2045 kJ. La diferencia de 2 kJ, debido a que a presión constante, una pequeña cantidad de trabajo de expansión es hecho contra la atmosfera ya que 6 mol de reactivos gaseosos son convertidos en 7 mol de productos gaseosos
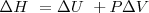
La oxidación de una grasa, como la tristearina a dióxido de carbono 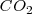 , el conjunto de la reacción es:
, el conjunto de la reacción es:
En esta reacción exotérmica hay un descenso en el volumen equivalente a la eliminación de 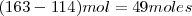 de gas producida por cada dos moles de tristearina que reaccionan. Debido a que el volumen del sistema decrece, la atmosfera (i.e. los alrededores del sistema) realiza un trabajo
de gas producida por cada dos moles de tristearina que reaccionan. Debido a que el volumen del sistema decrece, la atmosfera (i.e. los alrededores del sistema) realiza un trabajo 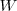 cuando la reacción procede. Esto es la energía es transferida al sistema cuan se contrae. Por esta razón el descenso de la energía interna del sistema es menor que la energía liberada como calor debido a que alguna energía ha sido restaurada en el sistema haciendo trabajo sobre él.
cuando la reacción procede. Esto es la energía es transferida al sistema cuan se contrae. Por esta razón el descenso de la energía interna del sistema es menor que la energía liberada como calor debido a que alguna energía ha sido restaurada en el sistema haciendo trabajo sobre él.
Para evitar la complicación de tener que tomar en cuenta la el trabajo de expansión se introduce una nueva función de estado 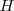 .
.
Una reacción endotérmica ( ) es aquella que tiene lugar a presión constante resulta en un incremento de entalpía (
) es aquella que tiene lugar a presión constante resulta en un incremento de entalpía ( 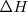 ) debido a que entra en el sistema como calor
) debido a que entra en el sistema como calor 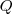 . Por otra parte, una reacción o proceso es exotérmico (
. Por otra parte, una reacción o proceso es exotérmico ( realizada a presión constante corresponde a un descenso en la entalpía (
realizada a presión constante corresponde a un descenso en la entalpía ( 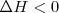 debido a que el sistema pierde energía como calor.
debido a que el sistema pierde energía como calor.
Las diferencias entre 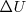 y
y 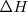 suelen ser generalmente pequeñas, por lo que las dos cantidades son casi iguales. Aunque la introducción de la entalpía tiene importantes consecuencias en termodinámica:
suelen ser generalmente pequeñas, por lo que las dos cantidades son casi iguales. Aunque la introducción de la entalpía tiene importantes consecuencias en termodinámica:
1.- Debido a que [Unparseable or potentially dangerous latex formula. Error 2 ] es una función de estado debído a que 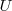

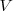 son funciones de estado, esto es su valor depende solo del estado actual del sistema no de la vía o caminos que ha tenido que tomar para llegar a él desde un estodo inicial.
son funciones de estado, esto es su valor depende solo del estado actual del sistema no de la vía o caminos que ha tenido que tomar para llegar a él desde un estodo inicial.
2.- El cambio de entalpía de un sistema puede ser identificado como el calor transferido a este a presión constante.
A presión constante, no hay trabajo de expansión: 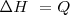 relación que es normalmente escrita como
relación que es normalmente escrita como
Si consideramos un sistema abierto a la atmosfera, así que la presión es constante y es igual a la 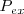
Teniendo en cuenta que el cambio de energía interna es dado por la ecuación:
(primer principio de la termodinámica) con
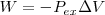
(dado que el sistema no realiza otra clase de trabajo). Si se sustituye esta expresión en la anterior se tiene que:
Donde el subíndice significa que la presión se mantiene constante. Por lo tanto imponiendo una restricción de presión constante, se identifica una observable cantidad (la energía transferida como calor) con un cambio en una función de estado la entalpía 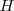 . Al tratar con funciones estado se simplifica el análisis termodinámico pues no hay que preocuparse sobre como ir de un estado a otro solo del estado inicial y final. Por ejmplo en el caso de la combustión de butano se puede escribir
. Al tratar con funciones estado se simplifica el análisis termodinámico pues no hay que preocuparse sobre como ir de un estado a otro solo del estado inicial y final. Por ejmplo en el caso de la combustión de butano se puede escribir 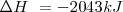 sin tener enguanta cuanto trabajo de expansión ha sido hecho.
sin tener enguanta cuanto trabajo de expansión ha sido hecho.
El cambio de energía interna  de un sistema que es libre para contraerse o expandirse (i.e. aumentar o disminuir su volumen) no es igual a la energía que es trasferida al sistema como calor (
de un sistema que es libre para contraerse o expandirse (i.e. aumentar o disminuir su volumen) no es igual a la energía que es trasferida al sistema como calor (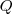 , debido a que alguna energía retorna de nuevo al exterior del sistema como trabajo (
, debido a que alguna energía retorna de nuevo al exterior del sistema como trabajo (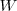 . No obstante el cambio de entalpía del sistema en estas condiciones es igual a la energía suministrada por calentamiento (i.e. como calor)
. No obstante el cambio de entalpía del sistema en estas condiciones es igual a la energía suministrada por calentamiento (i.e. como calor)
No es posible conocer sus valores absolutos (pues no se puede conocer los de la energía interna, 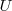 ) sino que sólo podemos calcular y medir sus variaciones
) sino que sólo podemos calcular y medir sus variaciones 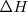 . Los valores de
. Los valores de 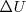 y
y 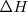 se suelen medir en condiciones estándar de presión y temperatura.
se suelen medir en condiciones estándar de presión y temperatura. 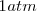 y
y 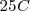 : en este caso, se representan con el superíndice
: en este caso, se representan con el superíndice  (por ejemplo
(por ejemplo