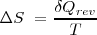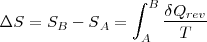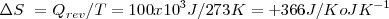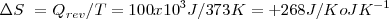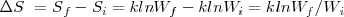Reversibilidad de las reacciones químicas. Segundo principio de la Termodinámica
De Wikillerato
En la naturaleza algunos procesos ocurren espontáneamente, por ejemplo un gas se expande hasta llenar todo el recipiente que lo continene, pero el gas en esa situación no se contrae súbitamente en un volumen más pequeño. Un objeto caliente se enfría a la temperatura de sus alrededores, pero nunca se observa que un objeto fría aparezca súbitamente más caliente que su entorno. El hidrógeno y el oxígeno se pueden combinar explosivamente (una vez que una chispa haya liberado su capacidad para hacerlo) para formar agua, pero el agua que compone los océanos, lagos y mares de la Tierra no se descompone gradualmente en hidrógeno y agua.
Estas observaciones sugieren que los cambios naturales pueden dividirse en dos clases:
Espontáneo: un cambio que tiene tendencia a ocurrir sin que sea necesaria la intervención exterior (en forma de trabajo).
Por ejemplo la combinación de hidrógeno en presencia de platino como catalizador:
La reacción en sentido directo ocurre espontáneamente, pero la reacción inversa, la descomposición del agua en sus elementos no ocurre espontáneamente independientemente del tiempo que esperemos para que ello ocurra.
No espontáneo: aquel que se realiza solo si es “instigado” o "dirigida" haciendo trabajo desde el exterior. Por ejemplo un gas puede ser comprimido por un pistón obligándolo a que ocupe menos volumen. Un objeto frío puede ser calentado por un calentador eléctrico. El agua puede ser descompuesta en hidrógeno y oxígeno por el pasaje de una corriente eléctrica (electrolisis).
La termodinámica trata con la tendencia al cambio, pero no dice nada de la tasa o velocidad en la cual esa tendencia es realizada. Así, algunos cambios espontáneos son muy rápidos tales como la reacción de precipitación que ocurre cuando soluciones de sal común 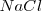 y nitrato de plata (
y nitrato de plata (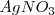 ) son mezcladas. Sin embargo, algunos cambios espontáneos son tan lentos que no hay un cambio observable después de millones de años. Por ejemplo aunque la descomposición del benceno en carbón e hidrógeno es espontánea, no ocurre en una tasa medible bajo condiciones normales.
) son mezcladas. Sin embargo, algunos cambios espontáneos son tan lentos que no hay un cambio observable después de millones de años. Por ejemplo aunque la descomposición del benceno en carbón e hidrógeno es espontánea, no ocurre en una tasa medible bajo condiciones normales.
Una reacción exotérmica ( 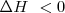 ) puede producirse espontáneamente por encontrar una situación más estable. Pero existen reacciones exotérmicas que no están de acuerdo con este criterio y otras endotérmicas que se producen de forma espontánea aunque sean endotérmicas, tal es el caso de la disolución de la sal común en agua. El hielo por ejemplo puede absorber espontáneamente calor del entorno y descongerlarse a temperaturas por encima del ºC. El gas
) puede producirse espontáneamente por encontrar una situación más estable. Pero existen reacciones exotérmicas que no están de acuerdo con este criterio y otras endotérmicas que se producen de forma espontánea aunque sean endotérmicas, tal es el caso de la disolución de la sal común en agua. El hielo por ejemplo puede absorber espontáneamente calor del entorno y descongerlarse a temperaturas por encima del ºC. El gas 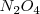 absorbe calor se descompone a
absorbe calor se descompone a 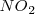 a 400 K .
a 400 K .
Todos estos procesos son endotérmicos, aunque todos son espontáneos. En todos los casos, el sistema se mueve espontáneamente a un estado de “más alta” energía potencial absorbiendo calor de sus alrededores.
Ya que algunas reacciones espontáneas son exotérmicas y otras endotérmicas la entalpía sola no puede dar cuenta para la dirección del cambio espontáneo, un segundo factor debe estar involucrado. Ese factor es la entropía, que relacionada adecuadamente con la entalpía, nos permite encontrar un criterio adecuado para estudiar la espontaneidad de un proceso o una reacción química.
Tabla de contenidos |
Entropía
El concepto de entropía (de la raíz griega ἐντροπία, el acto de cambio de dirección o vuelta y de (τροπη) transformación o cambio) es una cantidad termodinámica denotada con la letra S que fue introducido en 1865 en termodinámica por el científico alemán Rudolf J. E. Clausius (1822-1888) como en el análisis de la eficiencia de máquinas térmicas implicando la idea de reversibilidad .
La entropía 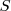 es una función de estado que nos indica el grado de desorden de un sistema. Así, como todas las demás funciones de estado que aparecen en termodinámica, la entropía es una medida en el actual estado de la dispersión de la materia y energía en el sistema, pero como el cambio fue alcanzado no es de importancia para el estado actual.
es una función de estado que nos indica el grado de desorden de un sistema. Así, como todas las demás funciones de estado que aparecen en termodinámica, la entropía es una medida en el actual estado de la dispersión de la materia y energía en el sistema, pero como el cambio fue alcanzado no es de importancia para el estado actual.
Matemáticamente, la variación de entropía 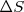 entre los estados A y B en un sistema termodinámico es igual al calor intercambiado (
entre los estados A y B en un sistema termodinámico es igual al calor intercambiado (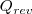 cuando se pasa de estado A a otro B mediante un proceso reversible dividido entre la temperatura absoluta:
cuando se pasa de estado A a otro B mediante un proceso reversible dividido entre la temperatura absoluta:
Si la variación es infinitesimal:
Entonces el cambio de entropía se calcula como:
En esta ecuación se usa 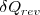 (una diferencial inexacta) en lugar de
(una diferencial inexacta) en lugar de 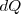 (una diferencial exacta), debido a que la tranferencia del calor calor
(una diferencial exacta), debido a que la tranferencia del calor calor 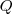 no es una función de estado (depende del camino en la misma). Por ello se utiliza matemáticamente
no es una función de estado (depende del camino en la misma). Por ello se utiliza matemáticamente 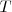 como un denominador de integración que sirve para convertir el elemento diferencial inexacto del calor
como un denominador de integración que sirve para convertir el elemento diferencial inexacto del calor 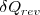 en el diferencial exacto de la función de estado S. Siendo
en el diferencial exacto de la función de estado S. Siendo 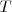 , la temperatura absoluta en la frontera del sistema donde el calor es transferido entre el sistema y su entorno y es por ello siempre positivo. El signo de la transferencia de entropía es el mismo que el signo de la transferencia de calor: positivo si se hace hacia el sistema y negativo si se hace hacia los alrededores.
, la temperatura absoluta en la frontera del sistema donde el calor es transferido entre el sistema y su entorno y es por ello siempre positivo. El signo de la transferencia de entropía es el mismo que el signo de la transferencia de calor: positivo si se hace hacia el sistema y negativo si se hace hacia los alrededores.
Las unidades de la entropía, en el Sistema Internacional (SI), son el J/K (o Clausius) definido como la variación de entropía que experimenta un sistema cuando absorbe el calor de 1 Julio (unidad) a la temperatura de 1 Kelvin.
Hay tres puntos de la ecuación ![[1] [1]](/images/math/math-5aa80f6cee65761be3342dbd4f17ccfe.png) que son necesarios destacar :
que son necesarios destacar :
a) El significado del término reversible (abreviadamente: rev) en 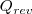 b) Por qué el calor (
b) Por qué el calor (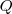 ) y no el trabajo (
) y no el trabajo (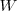 ) aparece en el numerador?
c) Por qué la temperatura aparece en el denominador?
) aparece en el numerador?
c) Por qué la temperatura aparece en el denominador?
a) Debido a que el calor 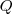 no es una función de estado, su valor dependerá del camino seguido para ir de A a B. En termodinámica se distinguen dos tipos de procesos termodinámicos:
no es una función de estado, su valor dependerá del camino seguido para ir de A a B. En termodinámica se distinguen dos tipos de procesos termodinámicos:
Procesos reversibles: son aquellos en el que el sistema permanece constantemente en equilibrio con el entorno. El camino del estado A al B se produce de forma infinitamente lenta; modificando ligeramente (idealmente de manera infinitesimal) las condiciones es posible revertir el proceso y regresar por el mismo camino de B al A; es por ello un proceso ideal. Dicho de otro modo, la reversibilidad se refiere a la habilidad de un cambio infinitesimal en una variable para cambiar la dirección de un proceso. Por ejemplo reversibilidad mecánica se refiere a la igualdad de la presión que actúa en cualquier lado de una parad móvil (e.g. un pistón). Reversibilidad térmica, se refiere a la igualdad de temperatura en cualquiera de los lados de una pared conductora del calor. El proceso es reversible porque al invertir el orden de las manipulaciones sobre el sistema termodinámico éste recorre, también de forma inversa un sucesión de estados de equilibrio termodinámico.
Procesos irreversibles: son aquellos que manifiestan una tendencia a producirse en un determinado sentido de manera espontánea. En ellos no existe equilibrio entre el sistema y el entorno y el sistema evoluciona de forma espontánea hasta alcanzarlo. No es posible detenerlo e invertir el proceso por el mismo camino. El paso de energía interna de un cuerpo caliente a otro más frío, el paso de un gas del recinto de mayor presión a otro, o la disolución de un colorante de una gota de tinta en el agua. La producción de calor por rozamiento es un proceso irreversible, pues no se puede invertir el proceso ya que se liberaría más energía en forma de calor, por rozamiento. En termodinámica la irreversibilidad se refiere generalmente al rápido calentamiento y o a la súbita realización de trabajo (por ejemplo el proceso de comprensión súbita de un gas es un proceso irreversible). Prácticamente todos los procesos naturales son irreversibles.
b) La primera ley de la termodinámica no hace distinción entre transferencia de energía como calor (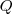 ) o como trabajo </math> W </math>, ambos eran considerados como iguales. La distinción entre
) o como trabajo </math> W </math>, ambos eran considerados como iguales. La distinción entre 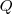 y
y 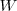 es realizada con la introducción de la entropía como función de estado.
es realizada con la introducción de la entropía como función de estado.
Una interacción energética la cual es acompañada por transferencia de entropía es una transferencia de calor, mientras que una interacción energética que no es acompañada con transferencia de entropía es el trabajo. Esto es, no se intercambia entropía durante una interacción entre un sistema y su entorno que involucra transferencia de energía en modo de trabajo. Así solo energía es intercambiada durante una interacción de trabajo, mientras que ambos energía y entropía son intercambiadas durante la transferencia de calor.
En términos moleculares (microscópicos) la transferencia de energía como calor se realiza con el movimiento desordenado de moléculas, mientras que la transferencia de la energía como trabajo, esta se realiza con movimientos moleculares ordenados. Por ello es posible que el cambio de entropía –el cambio en la dispersión de energía y de materia es proporcional a la energía transferencia que tiene lugar por el movimiento desordenado de moléculas más bien que movimientos ordenados. Esto es es el trabajo esta libre de generación de entropía
c) La presencia de T en el denominador tiene en cuenta la cantidad de desorden de movimiento que ya hay presente. Si una cantidad dada de energía es transferida como calor a un objeto caliente, la variación de entropía será menor que si la misma cantidad de energía calorífica es transferida a un objeto frío.
Por ejemplo:
La transferencia de 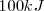 como calor
como calor 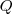 a una gran masa de agua (para asegurarnos que la temperatura del agua no cambie) a
a una gran masa de agua (para asegurarnos que la temperatura del agua no cambie) a 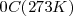 resulta en un cambio de entropía de:
resulta en un cambio de entropía de:
Por otra parte la misma transferencia de energía como calor a 100 ºC (373 k resulta en un cambio de:
El incremento de entropía es más grande a más baja temperatura. la entropía es una propiedad extensiva. La Entropía molar es una propiedad intensiva con unidades de 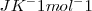 .
.
Entropía, orden, desorden y probabilidad
En 1896 el físico austríaco Ludwing Boltzmann (1844-1906) sugirió que la entropía (S) de un sistema está relacionada con el número de diferentes estados microscópicos (microestados) en el que puede estar. Los microestados de un sistema corresponden a una particular configuración (descrita en términos de velocidad posición de los constituyentes individuales-átomos, moléculas- ) de obtener una situación macroscópica estable y definida (microestado) del sistema. Así, un macroestado describe la situación del sistema desde un punto de vista macroscópico usando variables macroscópicas como la presión, la densidad, y la temperatura. Si el número de maneras equivalentes de construir una situación es 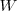 , entonces la entropía es proporcional a logaritmo neperiano de
, entonces la entropía es proporcional a logaritmo neperiano de 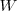 matemáticamente:
matemáticamente:
[Ecuación de Boltzmann]
Donde [Unparseable or potentially dangerous latex formula. Error 3 ]); [Unparseable or potentially dangerous latex formula. Error 3 ] , y 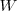 es la multiplicidad (grados de libertad) del sistema, también llamada probabilidad temodinámica o parámetro de desorden). Esto es a nivel microscópico
es la multiplicidad (grados de libertad) del sistema, también llamada probabilidad temodinámica o parámetro de desorden). Esto es a nivel microscópico 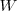 es el número de maneras equivalente en las que las moléculas pueden ser ordenadas para dar un mismo resultado o macroestado observable. Un estado desordenado es más probable que un estado ordenado, debido a que el estado desordenado se puede alcanzar de múltiples maneras. La ecuación de Botzmann nos da una precisa interpretación de la entropía en término de orden y desorden, proporciona una medida cuantitativa del desorden.
es el número de maneras equivalente en las que las moléculas pueden ser ordenadas para dar un mismo resultado o macroestado observable. Un estado desordenado es más probable que un estado ordenado, debido a que el estado desordenado se puede alcanzar de múltiples maneras. La ecuación de Botzmann nos da una precisa interpretación de la entropía en término de orden y desorden, proporciona una medida cuantitativa del desorden.
Con esta ecuación L. Boltzman hizo la crucial conexión entre entropía termodinámica y desorden. A partir de esta ecuación es claro que un incremento en 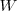 resulta en un incremento en S. Un cambio espontáneo en el macroestado de un sistema aislado está siempre acompañado por un incremento en
resulta en un incremento en S. Un cambio espontáneo en el macroestado de un sistema aislado está siempre acompañado por un incremento en 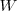 , por lo que siempre estará acompañado por un incremento de entropía Cuanta más alta es la entropía mayor es el desorden. La entropía es una medida de medida del desorden del sistema (i.e. la dispersión de su materia y energía del sistema)
, por lo que siempre estará acompañado por un incremento de entropía Cuanta más alta es la entropía mayor es el desorden. La entropía es una medida de medida del desorden del sistema (i.e. la dispersión de su materia y energía del sistema)
La diferencia de entropía entre dos estados microscópicos depende de la razón del número de posibles es estados microscópicos:
Para entender este resultado y como la ecuación de Boltzmann está relacionada con la probabilidad supongamos que tenemos un caja (mini-universo) de 20 monedas. Si agitamos la caja y observamos el resultado esperamos que el estado perfectamente ordenado (20 caras por ejemplo) es mucho menos probable que un estado desordenado donde las caras y cruces aparecen de manera azarosa. Ello es debido a que la probabilidad de los estados ordenados y desordenados es proporcional al número de maneras en las que el estado es alcanzado. Para alcanzar el estado perfectamente ordenado (20 caras) solo puede ser alcanzado de una manera al consistir en una única configuración. Por otra parte un estado desordenado se puede alanzan de múltiples maneras. Para veinte monedas el número de posible ordenamientos desordenados es 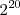 . Es por ello que la probabilidad de aparición de un estado desordenado es
. Es por ello que la probabilidad de aparición de un estado desordenado es 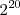 veces mayor que el estado ordenado.
veces mayor que el estado ordenado.
Supongamos ahora que nuestro mini universo es un cristal conteniendo moléculas de monóxido de carbono 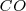 en las cuales el átomo de oxígeno corresponde a la cabeza de nuestra moneda y el átomo de carbono corresponde a la cruz de nuestra monedas anteriores. Supongamos que las moleculas estan orientadas en su eje mayor verticalmente y a una temperatura de
en las cuales el átomo de oxígeno corresponde a la cabeza de nuestra moneda y el átomo de carbono corresponde a la cruz de nuestra monedas anteriores. Supongamos que las moleculas estan orientadas en su eje mayor verticalmente y a una temperatura de 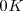 para mantener las moléculas en una configuración fijada. El ordenamiento de todas las moléculas de
para mantener las moléculas en una configuración fijada. El ordenamiento de todas las moléculas de 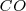 con los átomos de
con los átomos de 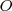 orientados hacia arriba puede ser obtenido en una sola vez, mientras que el estado desordenado con las cabezas de
orientados hacia arriba puede ser obtenido en una sola vez, mientras que el estado desordenado con las cabezas de 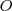 y colas de
y colas de 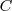 orientadas al azar puede ser igual a
orientadas al azar puede ser igual a 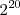 . Por lo tanto el estado desordenado del cristal es
. Por lo tanto el estado desordenado del cristal es 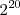 más probable que la estructura perfectamente ordenada. Si aplicamos la ecuación de Boltzamn a estas diferentes situaciones tenemos que:
más probable que la estructura perfectamente ordenada. Si aplicamos la ecuación de Boltzamn a estas diferentes situaciones tenemos que:
Para el estado ordenado con todas las moléculas de 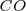 orientadas en la misma dirección:
orientadas en la misma dirección:
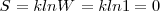
Para el estado desordenado (las moléculas de CO orientadas al azar)
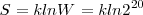 [Unparseable or potentially dangerous latex formula. Error 3 ]
[Unparseable or potentially dangerous latex formula. Error 3 ]
[Unparseable or potentially dangerous latex formula. Error 3 ]
[Unparseable or potentially dangerous latex formula. Error 3 ]
Si el cristal de 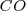 contiene 1 mol de moléculas de
contiene 1 mol de moléculas de 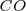 , la entropía del estado perfectamente ordenado ([Unparseable or potentially dangerous latex formula. Error 3 ] moléculas orientadas hacia arriba) sería cero, pero la entropía de un estado totalmente desordenado podría ser mucho más alta pues un número de avogadro de moléculas ([Unparseable or potentially dangerous latex formula. Error 3 ] puede ser organizado en un número enorme de maneras.
, la entropía del estado perfectamente ordenado ([Unparseable or potentially dangerous latex formula. Error 3 ] moléculas orientadas hacia arriba) sería cero, pero la entropía de un estado totalmente desordenado podría ser mucho más alta pues un número de avogadro de moléculas ([Unparseable or potentially dangerous latex formula. Error 3 ] puede ser organizado en un número enorme de maneras.
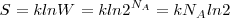
Debido a que 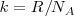
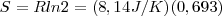
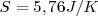
Basados en datos experimentales, la entropía de un mol (entropía molar) de monóxido de carbono sólido está cercana a 0K es aproximadamente de 5 J/K, indicando que las moléculas en el mismo adoptan un configuración casi al azar.
Segundo Principio de la Termodinámica
El primer principio de la termodinámica relaciona las diferentes formas de energía que intervienen en un proceso (e.g. una reacción química), pero no puede dar cuenta de la espontaneidad de un proceso, o la forma de producirse la misma, sin ayuda exterior. Se necesita algo que complete el primer principio, que nos informe sobre que procesos pueden ocurrir y cuales son imposibles. Este algo es el segundo principio de la termodinámica que afirma que:
La entropía total de cualquier sistema más la de su entorno (universo) se incrementa como resultado de cualquier proceso natural, o dicho de otra manera
La entropía del Universo se incrementa en el curso de cualquier cambio espontáneo que ocurre en él
Esto es matemáticamente:
[Unparseable or potentially dangerous latex formula. Error 3 ]
Esto es, todos los procesos que ocurren en el Universo constituyen un proceso neto adiabático. Considerando explícitamente la posibilidad de múltiples procesos se puede escribir:
La suma de los cambios entrópicos de un sistema y su exterior nunca puede disminuir:
[Unparseable or potentially dangerous latex formula. Error 3 ] = [Unparseable or potentially dangerous latex formula. Error 3 ] + [Unparseable or potentially dangerous latex formula. Error 3 ]
Donde 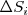 representa el cambio de entropía de un proceso individual. Esta inigualdad indica que los cambios de entropía asociados con un proceso individual
representa el cambio de entropía de un proceso individual. Esta inigualdad indica que los cambios de entropía asociados con un proceso individual 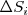 pueden ser positivos (
pueden ser positivos (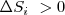 o negativos ([Unparseable or potentially dangerous latex formula. Error 3 ]) siempre que la suma del cambio de entropía para todos los procesos individuales que ocurran sea más grande cero.
o negativos ([Unparseable or potentially dangerous latex formula. Error 3 ]) siempre que la suma del cambio de entropía para todos los procesos individuales que ocurran sea más grande cero.
Esta ecuación proporciona una manera para determinar si un proceso es reversible, irreversible y permitido o irreversible y no permitido. Uno debe simplemente sumar todos los cambios de entropía en el Universo resultando del proceso. Cuando el cambio neto de entropía es cero [Unparseable or potentially dangerous latex formula. Error 3 ] el proceso es reversible, y entonces se dice que el sistema está en equilibrio. Si el cambio de entropía total es mayor que cero, el proceso puede ocurrir, diciéndose entonces que es un proceso espontáneo o natural. Si la entropía neta es menor que cero, el proceso no es espontáneo o no natural y no puede ocurrir. Así la segunda ley de la termodinámica proporciona un método importante para predecir la espontaneidad o reversibilidad de un proceso.
En cualquier real proceso espontáneo (incluyendo las reacciones químicas) el desorden del Universo siempre se incrementa. Así en cualquier sistema aislado, en la cual la energía total no cambia, una reacción es espontánea es aquella en la que la entropía ( y el desorden) se incrementa. Ningún proceso que produce orden, i.e. baja la entropía puede ocurrir sin la intervención o ayuda exterior.
En términos de probabilidad , las segunda ley de la termodinámica – la cual nos dice que la entropía incrementa en cualquier proceso, se reduce a la afirmación que aquellos procesos que ocurren son los más probables.Dicho de otro modo:
Los procesos naturales tienden a moverse hacia un estado de mayor desorden
Un importante aspecto de la segunda ley de la termodinámica es que nos dice también que en cualquier proceso natural irreversible alguna energía aparece no disponible para hacer trabajo útil. Así aunque la energía no se pierde como exige el primer pincipio de la termodinámica, pero aunque la energía no se pierde cuantitativamente si pierde cualidad i.e. es menos útil para hacer trabajo. La energía en este sentido se degradada, va de una forma más ordenda útil para hacer trabajo (tal como la mecánica) a otra forma eventualmente menos ordenada, energía interna o energía térmica. Una salida natural de este proceso a lo largo del tiempo sería la muerte térmica del Univeso, toda la energía del Universo se habría degradado en energía térmica, ningún trabajo sería posible de hacer, el Universo se encontraría en un estado de máximo desorden en equilibrio térmico.
References
.- Peter Atkins. Four Law. Oxford University Press. 2007.
.- Douglas C. Giancoli. Physics for Scientists and Engenineers with Modern Physics. Prentice Hall.1989.
.- Dilip Kondepudi an Ilya Progonine. Modern Thermodynamics. From Engines to Dissipative Structures. John Wiley & Son. 1998.
.- J. Bean Ott and Juliana Boerio-Goates. Chemical Thermodynamics. Principles and Applications. Elsevier Academic Press. 2000.
.- McMurry Fay. Chemistry.Pearson Education, Inc. 2004.
Enlaces externos
Entropy: [1]
Tweet


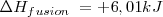
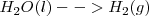
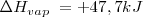

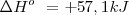
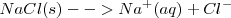
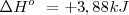
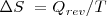
![[1] [1]](/images/math/math-095439d93d995dfe80bc45dbd2b54bda.png)