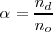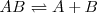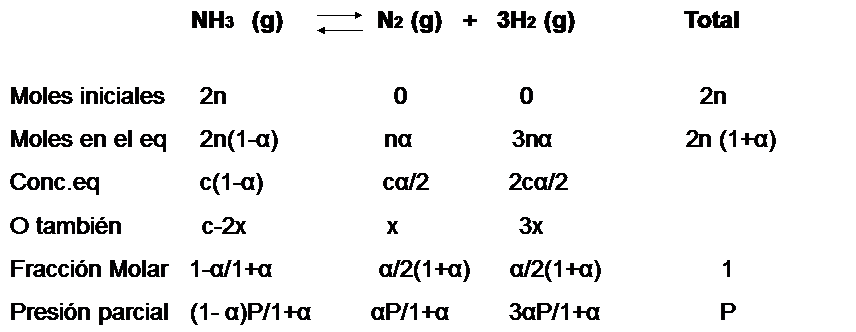La constante de equilibrio y el grado de disociación
De Wikillerato
El grado de disociación (representado por la letra griega 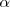 ) indica en tanto por uno (o en tanto %) de una sustancia que se disocia
) indica en tanto por uno (o en tanto %) de una sustancia que se disocia
donde 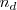 es el número de moles disociados y
es el número de moles disociados y 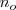 , es el número de moles totales
De esta manera en términos generales, para una disociación molecular, se puede expresar las concentraciones en el equilibrio en función del grado de disociación de la siguiente manera:
, es el número de moles totales
De esta manera en términos generales, para una disociación molecular, se puede expresar las concentraciones en el equilibrio en función del grado de disociación de la siguiente manera:
Una sustancia representada por [Unparseable or potentially dangerous latex formula. Error 3 ] y 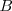 según la ecuación con la que se puede hacer la siguiente tabla:
según la ecuación con la que se puede hacer la siguiente tabla:
Moles iniciales n 0 0
Moles en el equilibrio (eq) n (1-α) nα nα
Concentración en el eq n (1-α) /V=c(1-α) nα/V=cα nα/V=cα O también c-x x x
Podemos aplicar así la constante de equilibrio de las concentraciones y calcular el grado de disociación α (tanto por uno de los moles de sustancia disociada o número de moles disociados a partir de una mol de sustancia inicial), o la fracción disociada  (cantidad disociada a parir de la cantidad inicial de sustancia)
(cantidad disociada a parir de la cantidad inicial de sustancia)
Por ejemplo:
Se puede expresar el progreso en la descomposición del amoniaco en nitrógeno y hidrógeno en términos del grado de disociación del amoniaco puro, el cual se disocia espontáneamente a una presión de 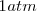 en un pequeña cantidad de nitrogeno (
en un pequeña cantidad de nitrogeno (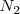 ) e hidrógeno
) e hidrógeno 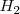 . La reacción de descomposición sigue la ecuación:
. La reacción de descomposición sigue la ecuación:
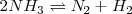
Se assume que comenzamos con amoniaco puro el experimento 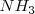 por lo que al inicio del mismo no tendremos ni nitrógeno ni hidrógeno. Ya que 2 moles de
por lo que al inicio del mismo no tendremos ni nitrógeno ni hidrógeno. Ya que 2 moles de 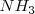 están invlucrados en la reacción tal cual está escrita, se asume que 2 moles de amoniaco están presente en el inicio. La descomposición de amoniaco en nitrógeno e hidrógeno avanza con el tiempo y en un mo derminado el sistema llega al equilibrio cuando una fracción
están invlucrados en la reacción tal cual está escrita, se asume que 2 moles de amoniaco están presente en el inicio. La descomposición de amoniaco en nitrógeno e hidrógeno avanza con el tiempo y en un mo derminado el sistema llega al equilibrio cuando una fracción 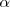 se ha disociado. Entonces de los
se ha disociado. Entonces de los 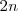 moles originales de
moles originales de 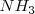 ,
, 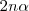 moles habrán descompuesto y
moles habrán descompuesto y 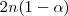 moles quedarán sin reaccionar.
moles quedarán sin reaccionar.
Por cada 2 moles de amoniaco que se descompone, 1 mol de nitrogeno y tres moles de hidrógeno se producen. En el equilibrio, los 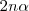 de amoniaco
de amoniaco 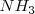 en descomposición producen
en descomposición producen 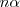 moles de
moles de 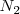 y
y 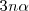 moles de hidrógeno. Así el número de total de moles de los tres tipos de moléculas se ha incrementado como resultado de la disociación. Ahora hay
moles de hidrógeno. Así el número de total de moles de los tres tipos de moléculas se ha incrementado como resultado de la disociación. Ahora hay 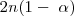 moles del gas, mientras que previo a la descomposición había solo [Unparseable or potentially dangerous latex formula. Error 3 ] moles.
moles del gas, mientras que previo a la descomposición había solo [Unparseable or potentially dangerous latex formula. Error 3 ] moles.
La fracción molar de cada componente en la mezcla de reacción se calcula dividiendo el número total de moles de cada componente por el número total de moles. Como podemos ver a ventaja de utilizar el grado de disociación 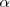 pues permite evitar de tratar con el número de moles
pues permite evitar de tratar con el número de moles  .
.
La constante de equilibrio para esta descomposición quedaría como:

Que se puede determinar termodinámicamente
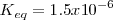
Usando este valor tenemos que:
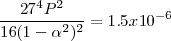
Después de combinar las constantes numéricas y tomando la raíz cuadrada de ambos lados, la ecuación queda
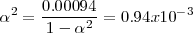
Esta expresión se puede resolver exactamente para 
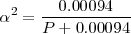
Ya que la presión P es de 1 atm se puede despreciar el término 0.00094 en el denominador y obtener la solución 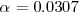 . Por lo tanto tenemos que a 298 K de temperaratura y ala presión de 1 atm el amoniaco
. Por lo tanto tenemos que a 298 K de temperaratura y ala presión de 1 atm el amoniaco 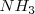 el amoniaco se encuentra un 3% aproximadamente disociado.
el amoniaco se encuentra un 3% aproximadamente disociado.