Sistemas de generadores y bases de un espacio vectorial
De Wikillerato
Tabla de contenidos |
Sistema generador
Un sistema generador de un espacio vectorial es un conjunto de vectores que tienen la propiedad de que cualquier vector del espacio vectorial es combinación lineal de los vectores del sistema generador.
Ejemplo
En
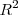 , los vectores
, los vectores
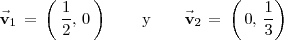
forman un sistema generador ya que cualquier vector
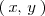 en
en
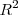 se puede poner como combinación lineal de
se puede poner como combinación lineal de
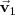 y
y
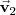 :
:
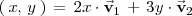
Base
Una base de un espacio vectorial es un sistema generador cuyos vectores son linealmente independientes.
Todas las bases de un mismo espacio vectorial tienen el mismo número de vectores y ese número se llama dimensión del espacio vectorial.
Todo espacio vectorial tiene, al menos, una base, y cualquier vector se puede expresar de forma única como combinació lineal de los vectores de la base.
Dada una base
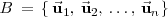
y un vector
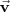 , éste se puede escribir de la siguiente forma:
, éste se puede escribir de la siguiente forma:
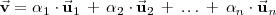
Los numeros
 reciben el nombre de coordenadas del vector
reciben el nombre de coordenadas del vector
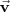 en la base
en la base
 .
.
Ejemplo
El vector
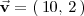 expresado en la base
expresado en la base
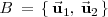 , siendo
, siendo
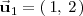 y
y
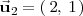 , es:
, es:
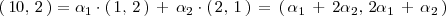
de donde:
![\left.
</p>
<pre> \begin{array}[c]{rcl}
\alpha_1 \, + \, 2 \alpha_2 & = & 10
\\
2 \alpha_1 \, + \, \alpha_2 & = & 2
\end{array}
</pre>
<p>\right\}
\, \Rightarrow \, \alpha_1 \, = \, -2, \, \alpha_2 \, = \, 6
\left.
</p>
<pre> \begin{array}[c]{rcl}
\alpha_1 \, + \, 2 \alpha_2 & = & 10
\\
2 \alpha_1 \, + \, \alpha_2 & = & 2
\end{array}
</pre>
<p>\right\}
\, \Rightarrow \, \alpha_1 \, = \, -2, \, \alpha_2 \, = \, 6](/images/math/math-a2e16dfae8192ee45eaf3762042f98c7.png)
Las coordenadas del vector
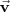 en la base
en la base
 son -2 y 6.
son -2 y 6.
Encualquier conjunto de 2 vectores linealmente independientes forman una base. En
cualquier conjunto de 3 vectores linealmente independientes forman una base.



