Propiedades de los determinantes

De Wikillerato

Revisión a fecha de 01:28 29 nov 2006; Fjmolina (Discutir | contribuciones)

(dif) ← Revisión anterior | Ver revisión actual (dif) | Revisión siguiente → (dif)

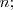
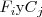En lo que sigue consideraremos $A$ como una matriz cuadrada de orden $n;$ $F_i \mathrm{y} C_j$ una fila o columna cualquiera de esa matriz.

El determinante de una matriz lo podemos ver como una funcion de sus filas

$\makebox{det} \left( A \right) = \left| A \right| = \makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_n \right)$

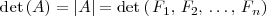
o de sus columnas

$\makebox{det} \left( A \right) = \left| A \right| = \makebox{det} \left( \, C_1, \, C_2, \, \ldots, \, C_n \right)$

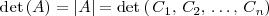
Las propiedades mas importantes de los determinantes son:

El determinante de una matriz cuadrada es igual al determinante de su matriz

traspuesta.

$\makebox{det} \left( A \right) = \makebox{det} \left( A^t \right)$

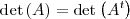
Si los elementos de una línea o columna de una matriz se multiplican por un número, el

determinante de la matriz queda multiplicado por dicho numero:

$\makebox{det} \left( \, C_1, \, C_2, \, \ldots, \, t \cdot C_j, \, \ldots, \, C_n \right) = t \cdot \makebox{det} \left( \, C_1, \, C_2, \, \ldots, \, C_j, \, \ldots, \, C_n \right)$

$\makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, t \cdot F_i, \, \ldots, \, F_n \right) = t \cdot \makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_i, \, \ldots, \, F_n \right)$

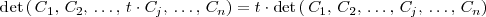
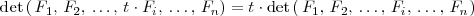
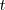Si todas las lineas de una matriz de orden $n$ están multiplicadas por un mismo número $t$ el determinante de la matriz queda multiplicado por $t^n:$

$\left| t \cdot A \right| = t^n \cdot \left| A \right|$

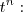
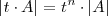
[Unparseable or potentially dangerous latex formula. Error 3 ]

$\makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_i + F_i^\prime, \, \ldots, \, F_n \, \right) <pre>\, = \, </pre> \makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_i, \, \ldots, \, F_n \, \right) <pre>\, + \, </pre> \makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_i^\prime, \, \ldots, \, F_n \, \right)$

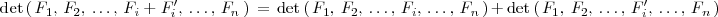
El determinante del producto de dos matrices cuadradas es igual al producto de los

determinantes de ambas matrices: $\makebox{det} \left( A \cdot B \right) = \makebox{det} \left( A \right) \cdot \makebox{det} \left( B \right)$

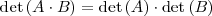
Si en una matriz cuadrada se permutan dos lineas, su determinante cambia de signo:

$\makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_i, \, \ldots, \, F_j, \, \ldots, \, <pre> F_n \, \right) </pre> = -\makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_j, \, \ldots, \, F_i, \, \ldots, <pre> \, F_n \, \right) </pre> $

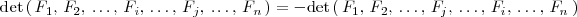
Si una línea de una matriz cuadrada es combinacion lineal de las lineas restantes, es

decir, es el resultado de sumar los elementos de otras lineas multiplicadas por números reales, su determinante es cero. Consecuencia inmediata de esta propiedad es que si una matriz tiene una línea de ceros su determinante es cero.

Si a los elementos de una línea de una matriz cuadrada se les suma una combinacion

lineal de las líneas restantes, su determinante no varia.

El metodo de Chío consiste en hacer cero el mayor número posible de elementos de una línea utilizando las propiedad anterior de los determinantes y posteriormente desarrollar el det

Obtenido de "http://wikillerato.org/Propiedades_de_los_determinantes.html"

Navegación

Herramientas

Buscar en WikilleratO

Propiedades de los determinantes

De Wikillerato