Matriz transpuesta

De Wikillerato

Se llama matriz traspuesta de una matriz     de dimension   ,   a la matriz que se obtiene al cambiar en     las filas por columnas o las columnas por filas. Se representa por 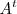    y su dimension es  

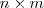
Propiedades:

• 
  •  
    •  
      •  

        
        

        ---

        
        

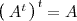
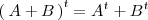
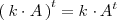
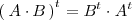
        Se llama matriz simetrica a toda matriz cuadrada     que coincide con su transpuesta:   .   En una matriz simetrica cualquier par de elementos simetricos respecto a la diagonal principal son iguales.

        Ejemplo:

        
        

        

        
        

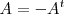        Se llama matriz antisimetrica a toda matriz cuadrada     que coincide con la opuesta de su transpuesta:   .   En una matriz simetrica cualquier par de elementos simetricos respecto a la diagonal principal son opuestos.

        Ejemplo:

        
        

        

        Obtenido de "http://wikillerato.org/Matriz_transpuesta.html"
           Tweet