Razones trigonométricas de la suma y diferencia de ángulos
De Wikillerato
Se puede demostrar que dados dos angulos
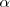 y
y
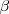 , el seno de su suma viene dado por la formula:
, el seno de su suma viene dado por la formula:
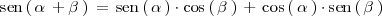
Si en la formula anterior sustituimos
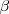 por
por
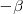 obtenemos:
obtenemos:
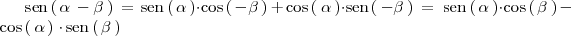
El coseno de la suma de los angulos
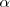 y
y
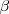 viene dado por la formula:
viene dado por la formula:
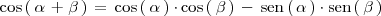
Si en la formula anterior sustituimos
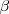 por
por
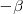 obtenemos:
obtenemos:
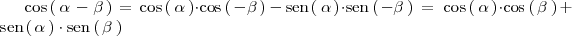
La segunda igualdad es cierta por las relaciones entre las razones trigonometricas de
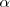 y
y
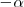 :
:
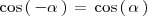
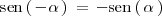
Si te preguntas porque esto es así, la respuesta la tienes [[Reducción de las razones trigonometricas|en esta sección]].



