Límite de una función
De Wikillerato
%% {{{ =limite
El límite de la función
 , cuando
, cuando
 tiende a
tiende a
 existe y es igual a
existe y es igual a
 , si ambos límites laterales existen y son iguales a
, si ambos límites laterales existen y son iguales a
 , es decir
, es decir
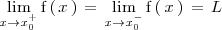
Lo expresamos de la siguiente manera:
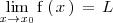
El que la anterior igualdad sea cierta significa que podemos hacer
 tan cercano a
tan cercano a
 como queramos eligiendo
como queramos eligiendo
 lo suficientemente proximo a
lo suficientemente proximo a
 , por la derecha o por la izquierda.
, por la derecha o por la izquierda.
Se dice que el límite de la funcion
 , cuando
, cuando
 tiende a
tiende a
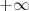 , es
, es
 si cualquier sucesión
si cualquier sucesión
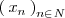 que tiende a
que tiende a
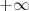 verifica que
verifica que
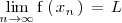 .
.
Lo expresamos como:
[Unparseable or potentially dangerous latex formula. Error 3 ]
El que la anterior igualdad sea cierta significa que podemos hacer
 tan cercano a
tan cercano a
 como queramos eligiendo
como queramos eligiendo
 lo suficientemente grande.
lo suficientemente grande.
Analogamente, se dice que el límite de la funcion
 , cuando
, cuando
 tiende a
tiende a
 , es
, es
 si cualquier sucesión
si cualquier sucesión
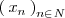 que tiende a
que tiende a
 verifica que
verifica que
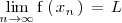 .
.
Lo expresamos como:
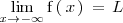
El que la anterior igualdad sea cierta significa que podemos hacer
 tan cercano a
tan cercano a
 como queramos eligiendo
como queramos eligiendo
 lo suficientemente pequeño.
lo suficientemente pequeño.
%% }}} %% {{{ =continuidad de funciones
Una función
 es continua en el punto
es continua en el punto
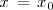 si
si
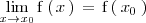 .
.
El que una función
 sea continua en el punto
sea continua en el punto
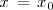 implica que
implica que
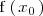 existe y que
existe y que
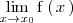 tambien existe.
tambien existe.
Una función es continua en un intervalo si es continua en todos los puntos del intervalo.
Una función es continua en todo su dominio cuando lo es en todos los puntos que lo componen.
%% }}} %% {{{ =discontinuidades
Tabla de contenidos[ocultar] |
Definición
Una función es discontinua en un punto
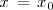 si
si
 no es continua en dicho punto.
no es continua en dicho punto.
Tipos de discontinuidades
Discontinuidad evitable
Una función
 tiene una discontinuidad evitable en un punto
tiene una discontinuidad evitable en un punto
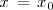 cuando existe el limite de la función en dicho punto.
cuando existe el limite de la función en dicho punto.
Ejemplo
La función
 definida por:
definida por:
![\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{x^2 \, - \, 1}{x \, - \, 1} & , &
\quad \makebox{si}\quad x \neq 1
\\
3 & , & \quad \makebox{si} \quad x \, = \, 1
\end{array}
</pre>
<p>\right.
\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{x^2 \, - \, 1}{x \, - \, 1} & , &
\quad \makebox{si}\quad x \neq 1
\\
3 & , & \quad \makebox{si} \quad x \, = \, 1
\end{array}
</pre>
<p>\right.](/images/math/math-1bc6370d459059982d4cbf56b3625528.png)
no es continua en el punto
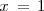 porque
porque
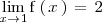 mientras que
mientras que
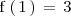 , es decir:
, es decir:
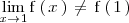
Como
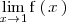 existe, la discontinuidad que
existe, la discontinuidad que
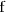 tiene en el punto
tiene en el punto
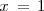 es evitable.
es evitable.
Discontinuidad de primera especie
Una función presenta una discontinuidad de primera especie en el punto
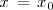 si los limites laterales de
si los limites laterales de
 en
en
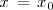 existen pero son distintos, es decir:
existen pero son distintos, es decir:
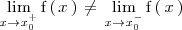
Ejemplo
La función
 definida por:
definida por:
![\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x^2 \, + \, 1 & , & \quad \makebox{si} \quad 1 \ge x
\\
x \, - \, 1 & , & \quad \makebox{si} \quad x \, > \, 1
\end{array}
</pre>
<p>\right.
\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x^2 \, + \, 1 & , & \quad \makebox{si} \quad 1 \ge x
\\
x \, - \, 1 & , & \quad \makebox{si} \quad x \, > \, 1
\end{array}
</pre>
<p>\right.](/images/math/math-b4e00ff82dd6d614ad2d9cc1fc106612.png)
no es continua en el punto
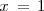 porque
porque
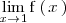 no existe, al ser ambos limites laterales distintos:
no existe, al ser ambos limites laterales distintos:
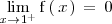
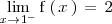
Como ambos limites laterales existen, la discontinuidad que
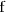 tiene en el punto
tiene en el punto
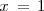 es de primera especie.
es de primera especie.
Discontinuidad de segunda especie
Una función
 presenta una discontinuidad de segunda especie en el punto
presenta una discontinuidad de segunda especie en el punto
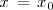 si no existe alguno de los limites laterales de
si no existe alguno de los limites laterales de
 en dicho punto.
en dicho punto.
Ejemplo
La función
 definida por:
definida por:
![\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{1}{x} & , & \quad \makebox{si} \quad 0 \ge x
\\
1 & , & \quad \makebox{si} \quad x \, > \, 0
\end{array}
</pre>
<p>\right.
\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{1}{x} & , & \quad \makebox{si} \quad 0 \ge x
\\
1 & , & \quad \makebox{si} \quad x \, > \, 0
\end{array}
</pre>
<p>\right.](/images/math/math-d50a20a5903b019c747f584dde612451.png)
no es continua en el punto
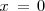 porque
porque
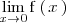 no existe, al no existir el limite por la izquierda de
no existe, al no existir el limite por la izquierda de
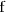 cuando
cuando
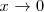 :
:
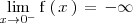
Como este limite por la izquierda no existe
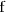 tiene en el punto
tiene en el punto
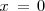 una discontinuidad de segunda especie.
una discontinuidad de segunda especie.



