Circunferencias tangentes de radio conocido
De Wikillerato
Lugares geométricos
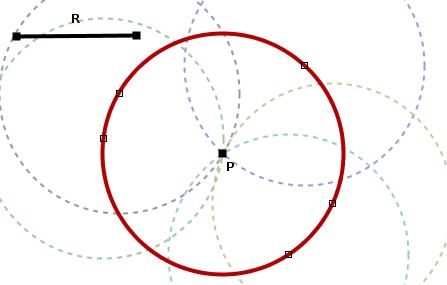
El lugar geométrico de los centros de todas las circunferencias de radio R conocido que pasan por un punto del plano fijo es la circunferencia con centro en el punto dado y radio R.
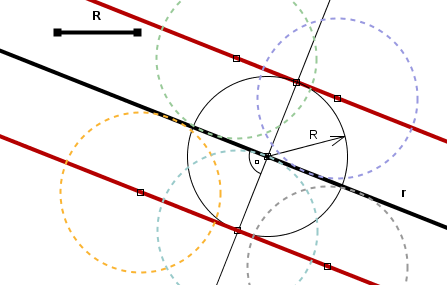
El lugar geométrico de los centros de todas las circunferencias de radio R conocido tangentes a una recta r dada son las dos rectas paralelas a r y situadas a una distancia R de la misma.
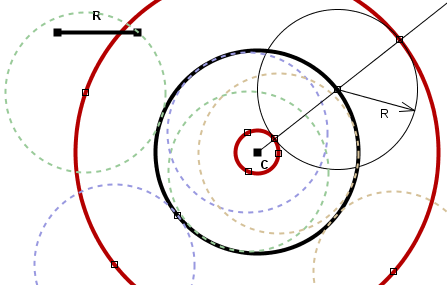
El lugar geométrico de los centros de todas las circunferencias de radio R conocido tangentes a una circunferencia de radio r dada son dos circunferencias concéntricas a la dada de radios R+r y |R-r|, respectivamente.
En efecto, si una circunferencia de radio R conocido ha de ser tangente a una recta o a una circunferencia dada, su centro deberá estar a una distancia de la recta o de la circunferencia igual a R. El lugar geométrico de los puntos que están a una distancia R de una recta dada son dos rectas paralelas a la recta dada, una a cada lado de la recta. Por su parte, el lugar geométrico de los puntos que están a una distancia R de una circunferencia dada son circunferencias concéntricas a la dada de radios R+r y |R-r|, siendo r el radio de la circunferencia dada. No importa cual de los radios R o r sea mayor; la expresión |R-r| siempre se interpretará como la diferencia entre el radio mayor y el radio menor.
En general, para dibujar una circunferencia de radio R conocido que sea tangente a dos elementos del plana o que pase por algún punto dado, habrá que determinar su centro como la intersección de dos de los lugares geométricos antes citados. En total, existen 6 casos diferentes, tal y como se detalla en los siguientes epígrafes.