Lógica proposicional
De Wikillerato
Una de las razones que motivó la aparición de la lógica matemática, fue evitar la ambigüedad del lenguaje natural y transformar el pensamiento en un cálculo, según el modo de operar de las matemáticas. Simplificar o simbolizar las oraciones o juicios para poder operar con ellas, así surge el
Tabla de contenidos |
Lenguaje formal
Consiste en abreviar o simbolizar las oraciones o juicios, que en la lógica matemática se llaman proposiciones. Estas proposiciones se reducen en el lenguaje formal a una sola letra, que llamamos variable, y la simbolizamos con las letras minúsculas del alfabeto que van de la “p” hasta el final del abecedario.
Si digo por ejemplo:”Antonio ama a Piedad”, esta proposición queda simbolizada en el lenguaje formal mediante la variable “p” o “q”, o “r”, o “s”.
Además de estas variables, la lógica proposicional utiliza otros símbolos, llamados constantes, cuyo significado siempre es el mismo ya que modifican o unen a las variables. Estos símbolos constantes, se llaman funtores, juntores, conectivas u operadores lógicos.
Cuando el funtor afecta a una sola variable, se llama monádico, como por ejemplo el negador (  ) que se lee en el lenguaje natural “no”, y se sitúa encima de la letra variable,
) que se lee en el lenguaje natural “no”, y se sitúa encima de la letra variable, 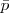 , “no p”. Cuando afectan a más de una variable, son poliádicos.
Los funtores más importantes son:
, “no p”. Cuando afectan a más de una variable, son poliádicos.
Los funtores más importantes son:
![[\land ] [\land ]](/images/math/math-baf992ff0c986159b9c5ef70e7e29e55.png) Conjuntor , “ y “ en el lenguaje natural.
Conjuntor , “ y “ en el lenguaje natural.
![[\lor ] [\lor ]](/images/math/math-bd8c0a940b89c20533d0b080b5224de6.png) Disyuntor , “ o “.
Disyuntor , “ o “.
![[\to ] [\to ]](/images/math/math-5c949e1f45fa0ca747c04cdf0101940c.png) Condicional, “ si…, entonces”.
Condicional, “ si…, entonces”.
![[\leftrightarrow ] [\leftrightarrow ]](/images/math/math-bb19fe548f207855642cd1fd75bb3aca.png) Bicondiconal, “ si y sólo si…, entonces”.
Bicondiconal, “ si y sólo si…, entonces”.
![[ \underline{\lor }] [ \underline{\lor }]](/images/math/math-104f5a0d465949a9bfad4cc2c89785df.png) Disyunción exclusiva, “o…o”, una proposición excluye a la otra.
Disyunción exclusiva, “o…o”, una proposición excluye a la otra.
El negador además de ser un funtor monádico, es decir que afecta a una variable, puede ser poliádico, cuando afecta a más de una variable o a una expresión entera.
Hay que tener siempre en cuenta, que las variables simbolizan oraciones enteras y no sólo palabras o nombres:
Ejemplos de simbolización de oraciones, del lenguaje natural al lenguaje formal:
1. La conjunción: ![[ p \land q ] [ p \land q ]](/images/math/math-2cd2ecd36dbd562c6b70fedbceb358ff.png) “Juan juega y Pedro estudia”.
“Juan juega y Pedro estudia”.
2. La disyunción: ![[ p \lor q ] [ p \lor q ]](/images/math/math-c919ef3ec2077fe7abd6e9a3bd7099cb.png) “Llueve o nieva”.
“Llueve o nieva”.
3. El condicional: ![[ p \to q ] [ p \to q ]](/images/math/math-202695fcd5d9899b7d9c76f19b3ca0a2.png) “Si estudias entonces aprendes”.
“Si estudias entonces aprendes”.
4. El bicondicional: ![[ p \leftrightarrow q ] [ p \leftrightarrow q ]](/images/math/math-53c3106d4bf4a887b9e0b5b1caf002c2.png) “Si y sólo si tienes dieciocho años puedes votar”.
“Si y sólo si tienes dieciocho años puedes votar”.
5. La disyunción exclusiva: ![[ p \underline{\lor} q ] [ p \underline{\lor} q ]](/images/math/math-768978eea6445529aa476b0cdc9d4f0a.png) “O te quedas o te vas”.
“O te quedas o te vas”.
6. La negación: ![[ \bar{p} ] [ \bar{p} ]](/images/math/math-4e0de1fd168b7d9b5d2909ae35ffdec9.png) “Manolo no juega limpio”.
“Manolo no juega limpio”.
A veces el negador puede afectar a más de una variable o a la conjunción, o disyunción de ambas:
![[\overline{p \lor q} ] [\overline{p \lor q} ]](/images/math/math-46b0a3ec03c3682d61fd6d350feefb3f.png) “Es falso que estudies o trabajes”.
“Es falso que estudies o trabajes”.
Valores de verdad
En la gramática estamos acostumbrados a ver que la oraciones pueden ser verdaderas o falsas, según se ajusten o no a la realidad que expresan, por ejemplo si llueve y digo que “hace sol”, esa oración es falsa. En cambio la lógica considera que las proposiciones pueden ser verdaderas o falsas con independencia de que en la realidad lo sean; por eso habla de valores de verdad.
Una proposición [  ] puede ser indistintamente verdadera o falsa; cuando es verdadera, le damos valor 1, cuando es falsa, le adjudicamos el valor 0.
Según esto la variable
] puede ser indistintamente verdadera o falsa; cuando es verdadera, le damos valor 1, cuando es falsa, le adjudicamos el valor 0.
Según esto la variable  , puede tener los siguientes valores:
, puede tener los siguientes valores:
 | |||
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
Cuando  siempre tiene valor 1, hablamos de tautología de
siempre tiene valor 1, hablamos de tautología de  . Cuando siempre es falsa, contradicción de
. Cuando siempre es falsa, contradicción de  . Si p es primero verdadera y luego falsa, afirmación de
. Si p es primero verdadera y luego falsa, afirmación de  . Cuando es primero falsa y luego verdadera, negación de
. Cuando es primero falsa y luego verdadera, negación de  .
.
Si consideramos los valores de dos variables conjuntamente, las posibilidades aumentan según el gráfico siguiente:
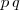 | ||||||||||||||||
| 1 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
Las dos primeras columnas indican los cuatro valores posibles que pueden tener dos proposiciones simples, si se consideran sus valores a la vez: las dos verdaderas, la primera verdadera y la segunda falsa, la primera falsa y la segunda verdadera y las dos falsas.
Las restantes dieciséis columnas representan los valores de verdad o falsedad, de cada una de las dieciséis proposiciones de orden dos.
Entre estas proposiciones, hay algunas que tienen especial interés en lógica, según los valores que adoptan las variables cuando están afectadas por funtores:
Proposición conjuntiva
 | 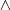 | 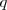 |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 0 | 0 |
La conjunción es verdadera sólo cuando ambas variables lo son y es falsa en los demás casos.
Se lee  y
y 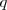 .
.
Proposición disyuntiva inclusiva
 | 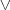 | 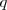 |
| 1 | 1 | 1 |
| 1 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
La disyunción es verdadera en todos los casos menos cuando  vale 1 y
vale 1 y 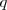 vale 0.
vale 0.
Se lee  ó
ó 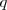 .
.
Proposición disyuntiva exclusiva
 | 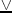 | 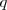 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
La disyunción exclusiva es verdadera cuando una variable es verdadera y la otra falsa, y es falsa en los demás casos.
Se lee  excluye a
excluye a 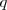 .
.
Proposición condicional
 |  | 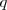 |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 1 | 0 |
El condicional es verdadero en todos los caso menos cuando  vale 1 y
vale 1 y 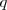 vale 0.
vale 0.
Se lee  condiciona a
condiciona a 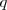 .
.
Proposición bicondicional
 |  | 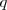 |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
El bicondicional es verdadero cuando ambos son verdaderos o cuando ambos son falsos, y es falso en los demás casos.
Se lee  bicondiciona a
bicondiciona a 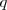 .
.
Proposición negativa
 | 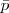 |
| 1 | 0 |
| 0 | 1 |
La negación - que se lee no  -, cambia el valor de la variable que se niega: sólo es verdadera si
-, cambia el valor de la variable que se niega: sólo es verdadera si  es falsa y es falsa si
es falsa y es falsa si  es verdadera.
es verdadera.
Proposiciones atómicas y moleculares. Las tablas de verdad ó tablas veritativas
En Química se aprende que los cuerpos están formados de átomos que se asocian formando moléculas; cuando una proposición consta de una sola variable la llamamos proposición atómica, y, cuando consta de muchas variables, proposición molecular.
Para hallar el valor de verdad de una proposición molecular, hay que descubrir el funtor capital, aquel que liga más, es decir que une o liga toda la expresión.
Un mecanismo sencillo para conocer el valor del funtor capital en una proposición molecular es el llamado método de las tablas de verdad.
Sirve de ayuda para localizar al funtor capital, la utilización de paréntesis y corchetes:
![[ (p \to q) \land p ] \to q [ (p \to q) \land p ] \to q](/images/math/math-b0b7d0454a86529ec7ea63427d1d198e.png)
En esta expresión se ve con claridad que el funtor capital es el condicional, que une todo el corchete con 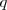 .
.
El modus operandi es ir encontrando el valor de verdad primero de los funtores que ligan menos, hasta llegar en último lugar al funtor capital.
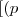 |
 |
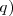 |
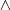 |
![p] p]](/images/math/math-15b46d537129816d89b6355753395739.png) |
 |
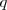 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 |
En esta expresión, se comienza hallando el valor del condicional en el primer paréntesis puesto que une a la  con la
con la 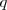 ; después la conjunción que une el resultado del condicional con la
; después la conjunción que une el resultado del condicional con la  dentro del corchete; y por último el condicional que une el resultado recién hallado de la conjunción con la última variable
dentro del corchete; y por último el condicional que une el resultado recién hallado de la conjunción con la última variable 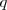 .
.
Cuando en la tabla aparece en todos los lugares de funtor capital el valor 1, la expresión es una tautología o identidad. Si en todos los lugares el valor es 0, es una contradicción. Finalmente cuando en el funtor capital encontramos valores de 1 y de 0, la proposición es indeterminada.
Dos proposiciones son equivalentes si tienen la misma tabla veritativa:
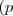 |
 |
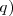 |
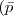 |
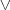 |
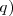 |
|
| 1 | 1 | 1 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 0 |
Según se observa en este ejemplo, el resultado del condicional en el primer paréntesis, es el mismo que el resultado de la disyunción en el segundo paréntesis. Estas proposiciones son por tanto, equivalentes; esto quiere decir que pueden ser sustituidas una por la otra.
Dada cualquier expresión, se puede sustituir por otra equivalente, esta afirmación se conoce con el nombre de principio o regla de sustitución.
Leyes lógicas
Todas aquellas proposiciones tautológicas son leyes de la lógica proposicional. Por ejemplo:
 |
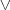 |
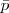 |
| 1 | 1 | 0 |
| 0 | 1 | 1 |
Es una ley lógica que ya conoció Aristóteles (384 – 322) con el nombre de tercero excluido o tertio excluso.
Las leyes lógicas son muy numerosas, pero hay algunas muy importantes que se refieren a la conjunción, disyunción y negador (La 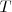 significa tautología y la
significa tautología y la  contradicción):
contradicción):
Idempotencia
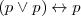
Asociativa
![[ ( p \lor q ) \lor r ] \leftrightarrow p \lor q \lor r [ ( p \lor q ) \lor r ] \leftrightarrow p \lor q \lor r](/images/math/math-b8b68b460f64c5b6d84c6cdee00a8e7d.png)
![[ ( p \land q ) \land r ] \leftrightarrow p \land q \land r [ ( p \land q ) \land r ] \leftrightarrow p \land q \land r](/images/math/math-90ef07ce091396816461cb7342344bb0.png)
Conmutativa
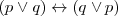
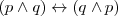
Identidad
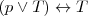
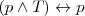
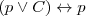
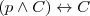
Absorción
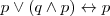
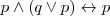
Distributiva
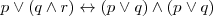
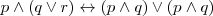
Negación
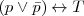
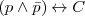
Morgan
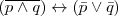
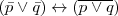
Doble negación
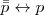
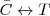
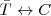
Para desarrollar la lógica proposicional no es necesario utilizar todos los funtores, es suficiente hacerlo con un número mínimo, son los funtores primitivos, a partir de los primitivos se obtienen los derivados.
La conjunción, disyunción y el negador son los primitivos, ya que gracias a la regla de sustitución, los demás funtores como el condicional o el bicondicional se pueden reducir a ellos:
Regla de sustitución
1. ![( p \leftrightarrow q ) \leftrightarrow [ ( p \to q ) \land ( q \to p ) ] ( p \leftrightarrow q ) \leftrightarrow [ ( p \to q ) \land ( q \to p ) ]](/images/math/math-3bd16d1cdd9721dc638cc38f85218394.png)
2. 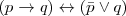
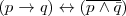
Ejercicios
Hallar la tabla veritativa de las siguientes expresiones:
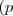 |
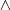 |
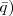 |
 |
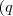 |
 |
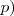 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 |



