Radicales
De Wikillerato
Tabla de contenidos |
Definición
Se llama enésima raíz, o raíz de orden n su función matemática función recíproca|recíproca.
Se puede anotar de las formas:
![y = \sqrt[n]{x} = x^{1/n} y = \sqrt[n]{x} = x^{1/n}](/images/math/math-ab489e28f676f42e3b8ed5e7a6501f50.png) .
.
Para todo n natural, a y b reales positivos, tenemos la equivalencia:
![a = b^n \iff b = \sqrt[n]{a} a = b^n \iff b = \sqrt[n]{a}](/images/math/math-e5625c799849d866eaf154d01265249b.png) .
.
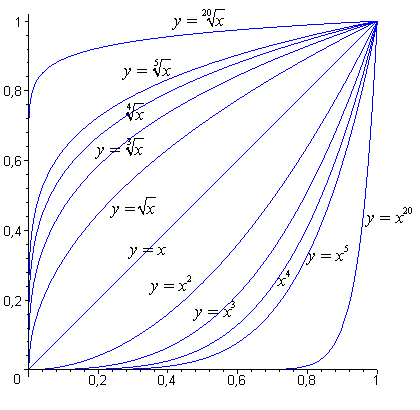
En él, se han dibujado las curvas de algunas raíces, así como de sus funciones recíprocas, en el intervalo [0;1]. La diagonal de ecuación y = x es eje de simetría entre cada curva y la curva de su recíproca.
Cambiando de escala:
La raíz de orden dos se llama raíz cuadrada y, por ser la más frecuente, se escribe sin superíndice: 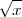 en vez de
en vez de ![\sqrt[2]{x} \sqrt[2]{x}](/images/math/math-c70166c527e8046753e3c221bbb57fbf.png) .
.
La raíz de orden tres se llama raíz cúbica.
El cálculo efectivo de la raíz se hace mediante las funciones logaritmo y exponencia:
![\sqrt[n]{x} = \exp\left(\frac{\ln {x}}{n}\right) = {e^{\frac {\ln x} n}} \sqrt[n]{x} = \exp\left(\frac{\ln {x}}{n}\right) = {e^{\frac {\ln x} n}}](/images/math/math-196b673388a7bd1170a9d50cb348c0b4.png) .
.
Todos los ordenadores y calculadoras emplean este método. El problema es que éste cálculo no funciona con los números negativos, porque el logaritmo usual sólo está definido en {0,+ ∞}. De ahí una tendencia, todavía minoritaria, de restringir la definición de las raíces de orden impar ![\sqrt[3]{x}, \sqrt[5]{x} ... \sqrt[3]{x}, \sqrt[5]{x} ...](/images/math/math-467b5c47141bb01c82dc7e95b9055564.png) a los números positivos.
a los números positivos.
Propiedades
Las propiedades de la radicación son bastante similares a las propiedades de la potenciación, puesto que una raíz es una potencia con exponente racional.
![\sqrt[n]{a} \sqrt[n]{a}](/images/math/math-a5bd4196465b30a2e2189804c2524662.png) =
= 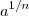 .
.
- Ejemplo
![\sqrt[4]{x^3} \sqrt[4]{x^3}](/images/math/math-09ec60d9272c52feb76d64c77ba59b1c.png) =
= 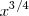 .
.
Raíz de un producto
|
- Ejemplo
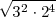 =
= 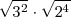 =
= 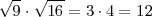
Se llega a igual resultado de la siguiente manera:
El 3 elevado a la dos dentro de la raiz cuadrada puede simplificarce quedando 3
Raíz de un cociente
|
- Ejemplo
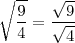 =
= 
Cuando esta propiedad se hace con números no hace falta pasar la raíz a potencia de exponente racional, aunque sí cuando se hace con variables.
![\sqrt[3]{\frac{x^3}{y^9}} = \frac{x^{3/3}}{y^{9/3}} \sqrt[3]{\frac{x^3}{y^9}} = \frac{x^{3/3}}{y^{9/3}}](/images/math/math-e36b3a8a87e6f51aa625a7a355728e36.png) =
= 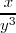
- Ejemplo
-
![(\sqrt[4]{a^2})^8 = (\ a^{2/4})^8 (\sqrt[4]{a^2})^8 = (\ a^{2/4})^8](/images/math/math-81e8e3407680caffde397c098ef20741.png) =
= ![\sqrt[4]{a^{16}} \sqrt[4]{a^{16}}](/images/math/math-6f2db5d271a830abbc7cfae6a891a737.png)
El tres elevado a las dos dentro de la raiz cuadrada puede simplificarce quedando 3
Raíz de una raíz
|
- Ejemplo
![\sqrt[9]{\sqrt[3]{5}} \sqrt[9]{\sqrt[3]{5}}](/images/math/math-5922d72ab064145bd9d879f7d43317b6.png) =
= ![\sqrt[27]{5} \sqrt[27]{5}](/images/math/math-d71bde628883b20dd126f586d0e121a7.png)
Como se indica con la igualdad ![y = \sqrt[n]{x^m} = x^{m/n} y = \sqrt[n]{x^m} = x^{m/n}](/images/math/math-72120c60a754ca55d7df7bc4fda9ad0a.png) , la radicación es en realidad otra forma de expresar una potenciación: la raíz de un cierto orden de un número es equivalente a elevar a dicho número a la potencia inversa.
, la radicación es en realidad otra forma de expresar una potenciación: la raíz de un cierto orden de un número es equivalente a elevar a dicho número a la potencia inversa.
La función raíz es creciente.
Por esto, las propiedades de la potenciación se cumplen también con la radicación. Tweet

![\sqrt[n]{{a} \cdot {b}} = \sqrt[n]{a} \cdot \sqrt[n]{b} \sqrt[n]{{a} \cdot {b}} = \sqrt[n]{a} \cdot \sqrt[n]{b}](/images/math/math-0eac084887ed59474e746958c4d0b87e.png) ;
;
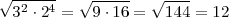
![\sqrt[n]{\frac{a}{b}} = \frac{a^{1/n}}{b^{1/n}} \sqrt[n]{\frac{a}{b}} = \frac{a^{1/n}}{b^{1/n}}](/images/math/math-839f98d9ffb9379957784ae8fe32559a.png) =
= ![\frac{\sqrt[n]{a}}{\sqrt[n]{b}} \frac{\sqrt[n]{a}}{\sqrt[n]{b}}](/images/math/math-fa0e43038224a0144da9a11b218711bc.png) ;
;
![\sqrt[n]{\sqrt[m]{a}} \sqrt[n]{\sqrt[m]{a}}](/images/math/math-735de0560a12e1e6688a47084c58a9cc.png) =
= ![\sqrt[n \cdot m]{a} \sqrt[n \cdot m]{a}](/images/math/math-95de20eeb87f53fee84b3deaf4f23a24.png) ;
;

