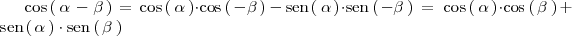Razones trigonométricas de la suma y diferencia de ángulos
De Wikillerato
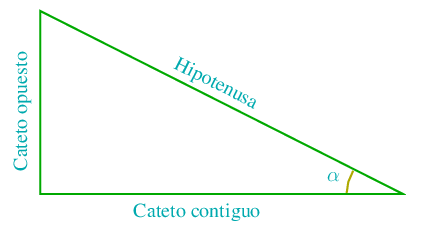
Dado un triángulo rectángulo, podemos estudiar las razones o proporciones entre sus lados.
Estas razones las definimos asociadas a cada uno de sus angulos de la siguiente forma:
El seno de un ángulo, es la razon entre su cateto opuesto y la hipotenusa. Su inversa es la cosecante:
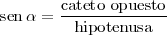
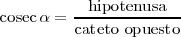
El coseno de un ángulo, es la razon entre su cateto contiguo y la hipotenusa. Su inversa es la secante:
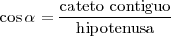
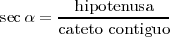
La tangente de un ángulo, es la razon entre su cateto opuesto y su cateto contiguo. Su inversa es la contangente:
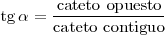
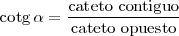
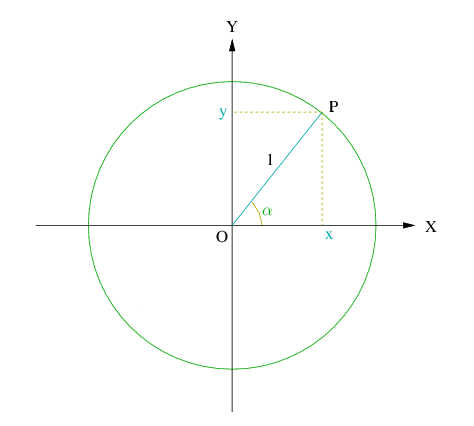
Para el estudio de las razones trigonometricas se suele considerar el angulo
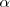 que forma el eje
que forma el eje
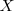 con el radio de una circunferencia de radio
con el radio de una circunferencia de radio
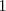 y centrada en el origen de coordenadas. A esta circunferencia se le llama
circunferencia goniometrica.
y centrada en el origen de coordenadas. A esta circunferencia se le llama
circunferencia goniometrica.
En este caso
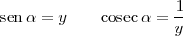

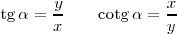
El angulo
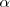 aumenta sii movemos el punto
aumenta sii movemos el punto
 en la circunferencia de manera que el radio
en la circunferencia de manera que el radio
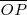 gire en sentido contrario al de las las agujas del reloj.
gire en sentido contrario al de las las agujas del reloj.
Si
 esta a la derecha del eje
esta a la derecha del eje
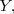 entonces
entonces
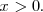 En caso contrario, se tiene que
En caso contrario, se tiene que
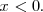 Si
Si
 esta por encima del eje
esta por encima del eje
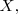 entonces
entonces
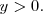 En caso contrario, se tiene que
En caso contrario, se tiene que
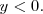
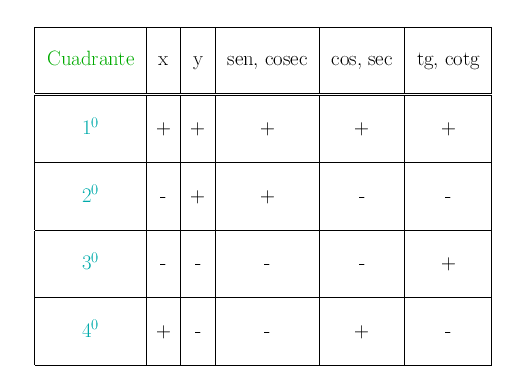
Los ejes de coordenadas dividen la circunferencia goniometrica en cuatro cuadrantes. El
signo de las razones de un angulo
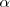 depende de en que cuadrante este situado
depende de en que cuadrante este situado
 . Todas las posibilidades estan recogidas en la tabla siguiente:
. Todas las posibilidades estan recogidas en la tabla siguiente:
%% }}} %% {{{ =suma y diferencia de angulos
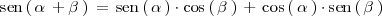
Si en la formula anterior sustituimos
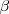 por
por
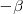 obtenemos:
obtenemos:
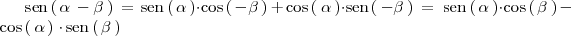
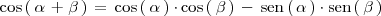
Si en la formula anterior sustituimos
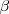 por
por
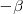 obtenemos:
obtenemos: