Triángulos
De Wikillerato
Tabla de contenidos |
Características generales
Un triángulo  es una figura plana limitada por tres rectas que se cortan dos a dos, determinando los segmentos
es una figura plana limitada por tres rectas que se cortan dos a dos, determinando los segmentos 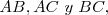 que son los lados del triángulo. Para que tres segmentos formen un triángulo
que son los lados del triángulo. Para que tres segmentos formen un triángulo  es necesario que cada uno de ellos sea menor que la suma de los otros dos y mayor que su diferencia.
es necesario que cada uno de ellos sea menor que la suma de los otros dos y mayor que su diferencia.
Nomenclatura de los triángulos
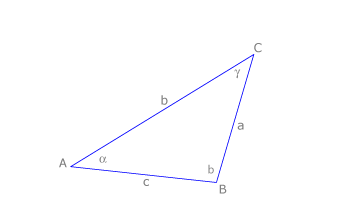
Los triángulos se nombran por sus vértices, 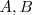 y
y  . El lado opuesto a cada vértice se llama como él, en minúscula: el vértice
. El lado opuesto a cada vértice se llama como él, en minúscula: el vértice  es opuesto al lado a, el
es opuesto al lado a, el  al
al 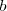 y el
y el  al
al  . Los ángulos pueden llamarse como el vértice:
. Los ángulos pueden llamarse como el vértice: 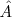 , con la letra griega
, con la letra griega 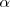 o indicando ordenadamente
o indicando ordenadamente 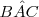 , donde
, donde  es el vértice.
es el vértice.
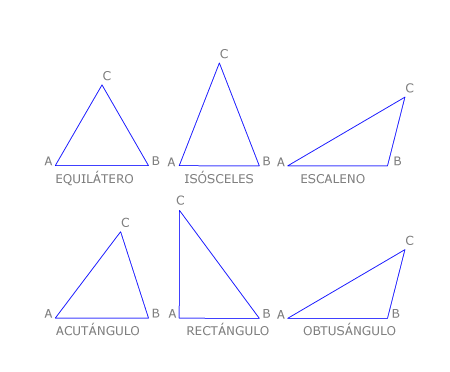
Los triángulos que tienen los tres lados iguales se llaman equiláteros. Esto implica que tengan tres ángulos iguales y tres ejes de simetría.
Los triángulos que tienen dos lados iguales se llaman isósceles. En este caso los lados iguales se llaman lados y el lado desigual se llama base. Los ángulos que tienen a la base como lado son iguales. Los triángulos isósceles sólo tienen un eje de simetría.
Los triángulos que no tienen lados iguales se llaman escalenos, sus ángulos son desiguales y no tienen ningún eje de simetría.
Los triángulos que tienen los ángulos agudos se llaman acutángulos.
Los triángulos que tienen un ángulo recto de llaman rectángulos. Los lados del ángulo recto se llaman catetos y el lado opuesto al ángulo recto se llama hipotenusa.
Los triángulos que tienen un ángulo obtuso se llaman obtusángulos.
Recordamos que la suma de los ángulos internos de un triángulo es de 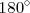 .
.
Concepto de identidad, igualdad y semejanza entre figuras
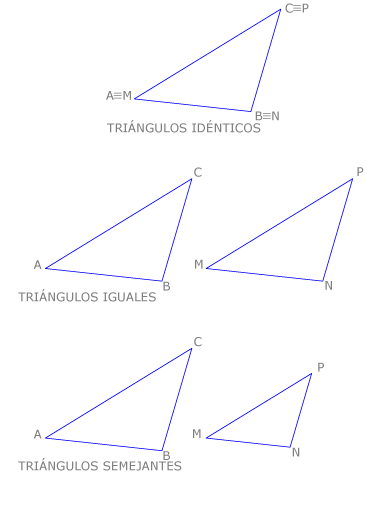
Dos figuras son idénticas cuando son iguales y ocupan el mismo lugar.
El signo de identidad es  . En nuestro ejemplo
. En nuestro ejemplo 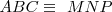 .
Dos figuras son iguales cuando tienen los lados iguales y los ángulos correspondientes iguales. El signo de igualdad es
.
Dos figuras son iguales cuando tienen los lados iguales y los ángulos correspondientes iguales. El signo de igualdad es  .
.
En nuestro ejemplo 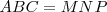 .
.
Dos figuras son semejantes cuando tienen los lados directamente proporcionales y los ángulos correspondientes iguales. En nuestro ejemplo 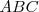 y
y 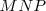 son triángulos semejantes.
son triángulos semejantes.
Concepto de equivalencia entre figuras
Dos figuras son equivalentes cuando tienen la misma superficie, aunque su forma sea distinta.
Teoremas relativos a los triángulos rectángulos
El teorema de Euclides
El teorema de Euclides tiene dos enunciados que conocemos con los nombres de teorema del cateto y teorema de la altura.
Teorema del cateto:”El cateto de un triángulo rectángulo es media proporcional entre la hipotenusa y su proyección sobre ella”.
Esto quiere decir que: 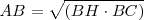 , lo que implica que:
, lo que implica que: 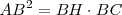
Teorema de la altura: “La altura relativa a la hipotenusa es media proporcional de las proyecciones de los catetos sobre ella”.
Esto quiere decir que: 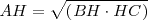 , lo que implica que:
, lo que implica que: 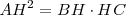
Vamos a demostrarlo.
El teorema de Pitágoras
El teorema de Pitágoras: “El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”.
Esto quiere decir que: 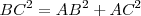 .
.
Una forma sencilla para entender el teorema de pitágoras es mediante el trazo de figuras, por lo que es necesario contar con una regla, compás, lápiz, papel y seguir éstos pasos. 1.- Traza una línea horizontal de 5cm de longitud. Ésta línea la llamaremos hipotenusa. 2.- Abre el compás 3cm, y traza un semicírculo por encima de la hipotenusa apoyándote en su extremo izquierdo. 3.- Abre el compás 4 cm y traza un semicírculo por encima de la hipotenusa apoyándote en su extremo derecho y buscando que cruce el semicírculo que trazamos en el punto 2. 4.- Une el punto de cruce de los semicírculos con cada uno de los extremos de la hipotenusa así formarás un triángulo rectángulo las dos líneas rectas trazadas les llamamos catetos. 5.- Sobre cada lado del trángulo le dibujamos un cuadrado usando las mismas dimensiones de los lados del triángulo. 6.- Cuadriculamos cada cuadrado en divisiones de 1 cm de lado. 7.- Observemos que el cuadrado de la hipotenusa tiene 25 cuadros, el cuadrado de un cateto tiene 9 cuadros, y el cuadrado del otro cateto tiene 16 cuadros.
Podemos concluir que el " El cuadrado de la hipotenusa (25) es igual a la suma de los cudarados de los catetos (16+9).
Demostraciones gráficas de los teoremas de Euclides y Pitágoras
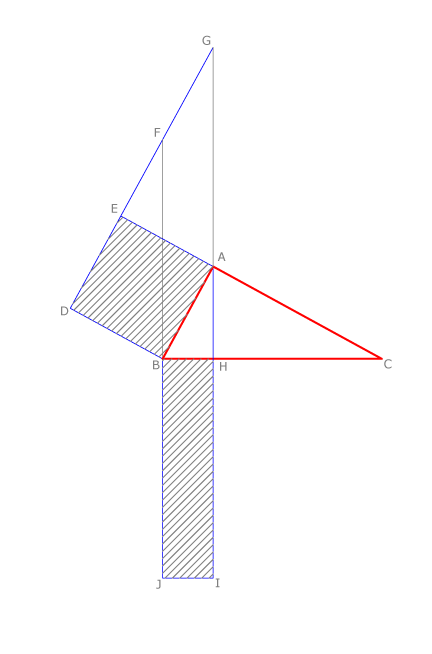
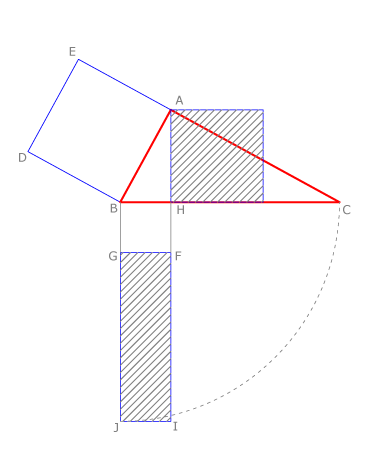
Vamos a demostrar en primer lugar el teorema de Euclides referente al cateto.
Consideramos un triángulo  rectángulo en
rectángulo en  . Dibujamos el cuadrado
. Dibujamos el cuadrado 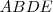 como se ve en la figura. Dibujamos la altura correspondiente a
como se ve en la figura. Dibujamos la altura correspondiente a  , siendo su pie el punto
, siendo su pie el punto 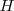 . Construimos el rectángulo
. Construimos el rectángulo 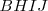 , siendo
, siendo  .
.
Se trata de demostrar que el cuadrado 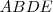 y el rectángulo
y el rectángulo 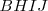 son equivalentes, es decir:
son equivalentes, es decir: 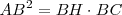 , como indica el teorema.
, como indica el teorema.
Prolongamos los lados 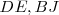 y
y 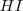 como indica la figura y obtenemos el paralelogramo
como indica la figura y obtenemos el paralelogramo 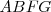 .
.
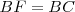 porque
porque 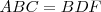 , pues los dos triángulos tienen un lado y dos ángulos iguales:
, pues los dos triángulos tienen un lado y dos ángulos iguales: 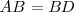 ; el ángulo
; el ángulo 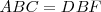 y los ángulos en
y los ángulos en  y en
y en 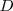 rectos. Recordamos que cuando se trazan perpendiculares a un ángulo se obtienen ángulos iguales o suplementarios.
rectos. Recordamos que cuando se trazan perpendiculares a un ángulo se obtienen ángulos iguales o suplementarios.
Comprobamos que 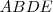 es equivalente a
es equivalente a 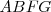 , porque los dos son paralelogramos con la misma base,
, porque los dos son paralelogramos con la misma base, 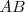 y la misma altura,
y la misma altura, 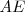 .
.
Por otra parte el rectángulo 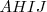 es equivalente
es equivalente 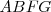 , porque los dos son paralelogramos con la misma base,
, porque los dos son paralelogramos con la misma base, 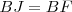 y la misma altura,
y la misma altura, 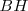 .
Por lo tanto, el cuadrado
.
Por lo tanto, el cuadrado 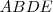 es equivalente al rectángulo
es equivalente al rectángulo 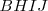 , como queríamos demostrar.
, como queríamos demostrar.
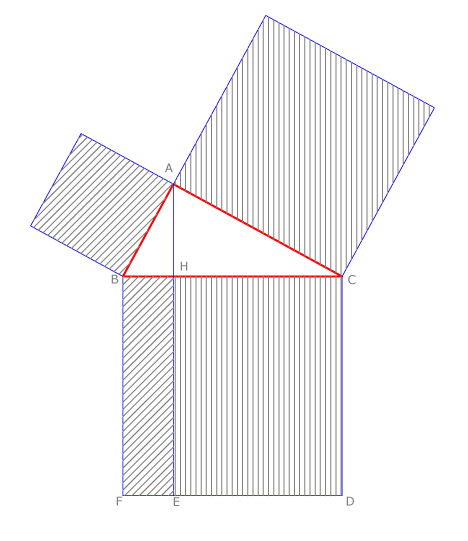
Demostramos a continuación el Teorema de Pitágoras. En el triángulo  de la figura debemos demostrar que
de la figura debemos demostrar que 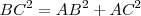 .
.
Aplicamos el teorema del cateto. Recordamos su demostración y vemos que el cuadrado de lado 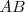 es equivalente, es decir, es de la misma superficie que el rectángulo
es equivalente, es decir, es de la misma superficie que el rectángulo 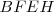 . Por el mismo teorema, el cuadrado de lado
. Por el mismo teorema, el cuadrado de lado 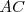 es equivalente al rectángulo
es equivalente al rectángulo 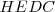 . Como la suma de dichos rectángulos es igual al cuadrado de lado igual a la hipotenusa, el teorema queda demostrado.
. Como la suma de dichos rectángulos es igual al cuadrado de lado igual a la hipotenusa, el teorema queda demostrado.
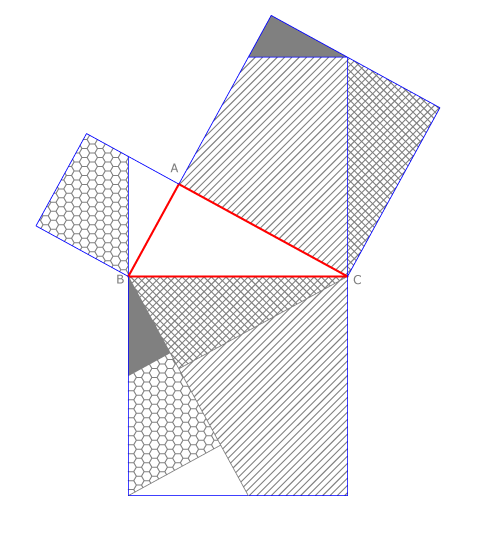
El teorema de Pitágoras se puede demostrar también haciendo equiparticiones de los cuadrados, es decir, dibujándolos y dividiéndolos en partes iguales entre sí. Hay muchos modos de hacerlo. En la figura vemos uno de ellos. Las partes iguales están rayadas del mismo modo.
Vamos a demostrar finalmente el teorema de Euclides referente a la altura.
Consideramos un triángulo  rectángulo en
rectángulo en  . Dibujamos el cuadrado
. Dibujamos el cuadrado 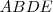 como se ve en la figura. Dibujamos la altura correspondiente a
como se ve en la figura. Dibujamos la altura correspondiente a  , siendo su pie el punto
, siendo su pie el punto 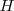 .
.
Se trata de demostrar que 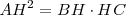 , como indica el teorema.
, como indica el teorema.
Aplicamos el teorema de Pitágoras en el triángulo rectángulo 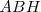 . Dibujamos los cuadrados de lados
. Dibujamos los cuadrados de lados 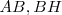 y
y 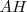 .
.
Se cumplirá que 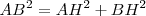 , luego:
, luego: 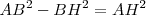 .
.
Por el teorema del cateto sabemos que el cuadrado de lado 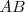 es equivalente al rectángulo de lados
es equivalente al rectángulo de lados 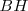 y
y 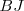 en el que
en el que  . Si restamos de dicho rectángulo el cuadrado de lado
. Si restamos de dicho rectángulo el cuadrado de lado 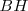 el teorema queda demostrado, pues
el teorema queda demostrado, pues 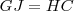 .
En la figura vemos que las dos figuras equivalentes están rayadas.
.
En la figura vemos que las dos figuras equivalentes están rayadas.
Teorema relativo al triángulo equilátero
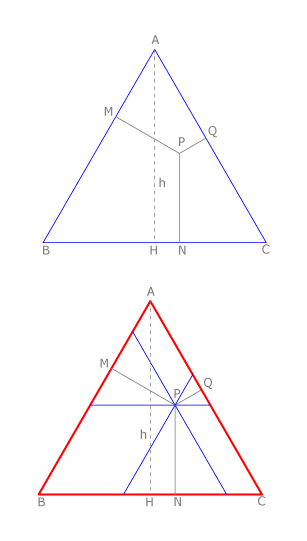
Teorema de Viviani:”En un triángulo equilátero la suma de las distancias desde un punto interior P a los lados del triángulo es igual a la altura del triángulo”.
Si el punto  fuera exterior la relación se cumple siempre que se consideren negativas una o dos distancias.
fuera exterior la relación se cumple siempre que se consideren negativas una o dos distancias.
Vamos a hacer una demostración gráfica de este teorema, trazando paralelas a los lados del equilátero por el punto  . Definimos así tres equiláteros, como vemos en la figura. Recordando que en los paralelogramos los lados opuestos son iguales, es fácil comprobar que la suma de los lados de estos triángulos es igual al lado de
. Definimos así tres equiláteros, como vemos en la figura. Recordando que en los paralelogramos los lados opuestos son iguales, es fácil comprobar que la suma de los lados de estos triángulos es igual al lado de  . Por lo tanto, la suma de sus alturas será igual a la altura de
. Por lo tanto, la suma de sus alturas será igual a la altura de  .
.
Teoremas relativos a todos los triángulos
Estos dos teoremas pueden generalizarse a todos los polígonos equiláteros y equiangulares.
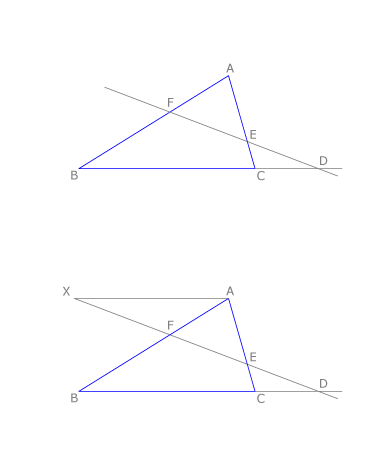
Teorema de Menelao
“Si  es un triángulo y
es un triángulo y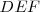 una recta que corta sus tres lados en
una recta que corta sus tres lados en 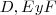 , se verifica que:
, se verifica que:
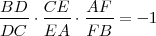 ”.
”.
La razón es negativa porque uno de los tres puntos de intersección estará siempre en el exterior del triángulo y su distancia al vértice se considerará negativa. En nuestro ejemplo será negativo 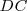 .
.
Vamos a demostrarlo. Trazamos por  una paralela a
una paralela a 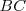 . Prolongamos la recta y hallamos el punto
. Prolongamos la recta y hallamos el punto 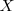 . Se forman dos pares de triángulos semejantes:
. Se forman dos pares de triángulos semejantes: 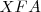 y
y 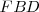 ;
; 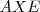 y
y 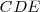 .
.
Fijándonos en estos triángulos tenemos que:
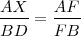 y
y 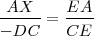 , luego
, luego
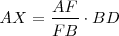 , por la otra igualdad:
, por la otra igualdad:
 ; luego:
; luego:
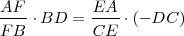 , lo que implica que:
, lo que implica que:
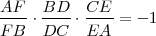 , como afirma el teorema.
, como afirma el teorema.
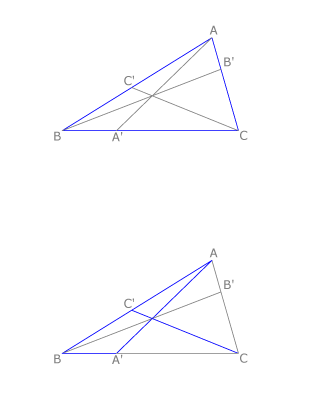
Teorema de Ceva
“La condición necesaria y suficiente para que sean concurrentes tres rectas trazadas desde los vértices 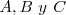 de un triángulo a los puntos
de un triángulo a los puntos 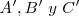 de los respectivos lados opuestos es que:
de los respectivos lados opuestos es que:
 ”.
”.
Este teorema está íntimamente ligado al de Menelao. Para demostrarlo se consideran los triángulos 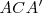 y
y 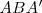 cortados respectivamente por
cortados respectivamente por 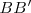 y
y 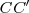 .
.
Este teorema se utiliza para demostrar que las alturas, las medianas y las bisectrices de todo triángulo son concurrentes.
Toda recta que pasa por el vértice de un triángulo toma el nombre de ceviana de este teorema
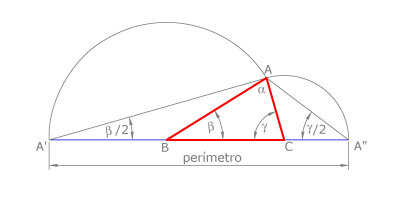
Propiedad relativa al perímetro de los triángulos
Sea el triángulo  . Si llevamos las magnitudes
. Si llevamos las magnitudes 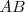 y
y 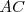 sobre la prolongación de
sobre la prolongación de 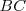 , trazando los arcos de centro
, trazando los arcos de centro 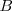 y radio
y radio 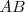 y centro
y centro  y radio
y radio 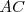 , como indica la figura, obtenemos un triángulo
, como indica la figura, obtenemos un triángulo 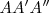 que tiene como lado
que tiene como lado 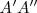 el perímetro del triángulo, ángulo en
el perímetro del triángulo, ángulo en 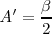 y ángulo en
y ángulo en 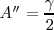 , siendo
, siendo 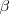 y
y 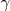 los ángulos en
los ángulos en 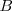 y en
y en  del triángulo.
del triángulo.
Esta propiedad es interesante cuando se debe resolver un problema cuyos datos sean o bien el perímetro o bien la suma de dos de los lados de un triángulo.
Tweet