Cajas de resonancia: Instrumentos musicales
De Wikillerato
Los aparatos destinados a producir o a analizar los sonidos están basados en la teoría de las ondas estacionarias, o casi estacionarias.
Un sistema rigurosamente estacionario no emitiría sonido alguno. Por el contrario, un sistema casi estacionario, generalmente muy amortiguado, que juega el papel de excitador, acoplado a una cavidad resonante, puede generar un sonido audible. Irradia así una onda progresiva que es percibida por el oído o un micrófono.
Tanto para los modos de vibración de las cuerdas, como de las ondas longitudinales en un resorte, la longitud del resonador y la frecuencia de vibración del foco acordados, al cumplir determinadas condiciones, permiten al resonador alcanzar una gran amplitud. Esta propiedad adquiere verdadera relevancia en acústica, pues, a menudo, las vibraciones sonoras llegan al oído con una amplitud y una compresión muy pequeñas y, a causa de ello, no provocan ninguna sensación sonora. Sin embargo, si reducimos el tiempo de funcionamiento de un foco sonoro, que ha emitido un sonido con una cierta cantidad de energía, podemos hacer que comunique esa energía a un resonador que durante un cierto tiempo sea capaz de irradiar una potencia suficiente para que el sonido pueda ser oído.
Tabla de contenidos[ocultar] |
Experiencias con cavidades resonantes
Cuando golpeamos un diapasón separado de su caja de resonancia, las vibraciones se mantienen durante un cierto tiempo – la amortiguación es más débil- pero el sonido es apenas audible.
Pero si acoplamos el diapasón a su cavidad de resonancia, la intensidad del sonido es mucho mayor pero se apaga muy rápidamente – el amortiguamiento es muy grande- .Se ha producido un acorde entre la frecuencia del diapasón y la frecuencia propia de la masa de aire contenido en la caja. El diapasón ha comunicado al aire de la caja suficiente energía para que su amplitud aumente e irradie una potencia suficiente hacia el auditor.
El teorema de conservación de la energía permite prever que la duración de este movimiento sea sensiblemente más corto que cuando se hace vibrar al diapasón sólo. Para la misma energía, si la potencia es mayor el tiempo ha de ser necesariamente menor. El aire contenido en la caja de resonancia del diapasón constituye un sistema discreto.
La caja de un violín resuena porque las cuerdas vibrantes transmiten sus vibraciones por medio del puente o ponticello. Si se quiere que las vibraciones de la caja duren deben ser mantenidas por el movimiento del arco.
En los casos descritos, se trata de frecuencias propias de resonancia formando un conjunto discreto.
Dos diapasones idénticos A y B, cuyas cajas de resonancia se encuentran enfrentadas por sus caras abiertas, a una corta distancia, nos permiten “oir” la transmisión de la potencia de la resonancia. Hacemos vibrar A, el aire A´ contenido en su caja transmite sus vibraciones al aire contenido en B´ que a su vez hace vibrar B. Si tocamos A con un dedo, para que deje de vibrar, B sigue vibrando, y si dejamos A libre, éste comenzará a vibrar de nuevo.
Naturalmente la intensidad de las vibraciones emitidas por A será mucho menor, pues la energía se encuentra ya muy repartida.
Una cavidad de resonancia esférica de radio adecuado, puede entrar en resonancia excitada por un diapasón. El aire contenido en la esfera se encuentra entonces animado por movimientos intensos y, colocando el orificio estrecho del resonador cerca del conducto auditivo, se oirá muy reforzado un sonido inaudible sin este artificio.
Es la experiencia más interesante pues nos permite, al igual que un Tubo de Kundt, medir la velocidad del sonido en el aire. Un tubo de vidrio limita una columna de aire cuya altura podemos hacer variar lentamente poniendo en juego la teoría de los vasos comunicantes.
Haciendo vibrar el diapasón cerca de la boca del tubo, el sonido se escucha claramente reforzado para una determinada longitud de la columna de aire. Si hacemos mayor la longitud de la columna no nos llegará más sonido que el procedente del diapasón, es decir, muy debilitado. Hasta que, si seguimos bajando el nivel del agua, aparece el sonido de nuevo reforzado. La distancia entre las dos posiciones en las que se escucha resonancia en el tubo es media longitud de onda.
La experiencia puede hacerse también con un altavoz pequeño conectado a un generador de baja frecuencia. En este caso, manteniendo la longitud de la columna, podemos hacer variar la frecuencia del generador hasta encontrar otros máximos que, como veremos a continuación, serán los armónicos de un tubo de esa longitud.
Armónicos de los tubos resonantes
La explicación de la experiencia anterior es la misma que la encontrada para las cuerdas. En este caso, podemos encontrar dos posibilidades: 1) Tubo abierto por los dos extremos; 2) Tubo cerrado por un extremo.
En los dos casos la capa de aire próxima a la boca de los tubos presenta un vientre de desplazamiento, en los que la energía cinética de las partículas es máxima. Sin embargo, en los tubos cerrados por un extremo, en el extremo cerrado aparece un nodo de desplazamiento, que son vientres de presión.
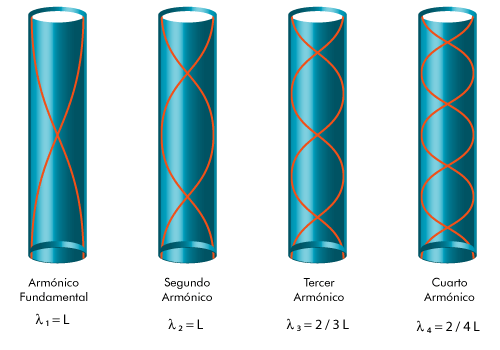
Tubo abierto por los dos extremos
Al tratarse de tubos abiertos en los dos extremos, colocando en la proximidad de una de las bocas el altavoz conectado a un GBF, escucharemos el sonido reforzado cuando 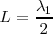 . Lo llamamos primer armónico o armónico fundamental.
. Lo llamamos primer armónico o armónico fundamental.
Haciendo variar la frecuencia, el siguiente armónico o sobre tono del tubo corresponderá a una longitud de onda tal que 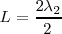 , lo llamamos segundo armónico o primer sobre tono; el siguiente para
, lo llamamos segundo armónico o primer sobre tono; el siguiente para 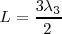 , que será el tercer armónico o segundo sobretodo; el siguiente para
, que será el tercer armónico o segundo sobretodo; el siguiente para 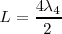 , etc.
, etc.
De un modo general encontramos que: 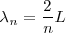
Vemos que las longitudes de onda van siendo cada vez más cortas y, por lo tanto, las frecuencias más altas.
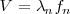
de modo que
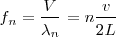
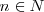
Que cada vez van siendo más altas, los sonidos más agudos.
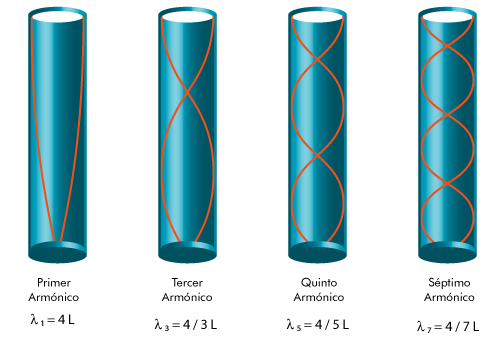
Tubos cerrados por un extremo
Al tratarse de un tubo cerrado por un extremo, en éste siempre habrá un nodo de desplazamiento y, por lo tanto, un vientre de presión acústica. El extremo abierto será un vientre de desplazamiento y un nodo de presión.
El armónico fundamental se corresponde con 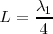 . Al hacer variar la frecuencia encontraremos el tercer armónico - no se habla de segundo, cuarto, armónicos en los tubos cerrados por un extremo- para
. Al hacer variar la frecuencia encontraremos el tercer armónico - no se habla de segundo, cuarto, armónicos en los tubos cerrados por un extremo- para 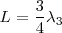 .
.
Del mismo modo el quinto armónico para 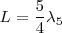 , etc.
, etc.
Cada vez la longitud de onda va siendo más corta y el sonido será más agudo.
De un modo general
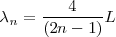
con 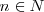
De igual modo para las frecuencias,
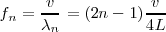
Vemos pues que las frecuencias propias de resonancia sólo pueden tomar valores discretos.