Ecuación de las ondas armónicas
De Wikillerato
a) Doble periodicidad
Pero veamos cómo varía, en función del tiempo, la magnitud característica de la perturbación que se propaga en el medio. Para ello consideraremos, un punto M, situado en la abcisa x del medio (siendo OM la distancia al origen de la cuerda o al foco emisor en la superficie del agua)
Sabemos que 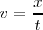 siendo t el tiempo que tarda la perturbación en alcanzar el punto x.
siendo t el tiempo que tarda la perturbación en alcanzar el punto x.
Pero también
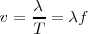 , de donde
, de donde 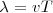
Como ya se vio en el estudio del movimiento oscilatorio armónico, el punto 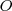 , lugar donde situamos al foco emisor, oscila de acuerdo con la ecuación:
, lugar donde situamos al foco emisor, oscila de acuerdo con la ecuación:
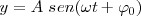
Para hacer más sencillos los cálculos consideraremos momentáneamente que 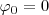 .
.
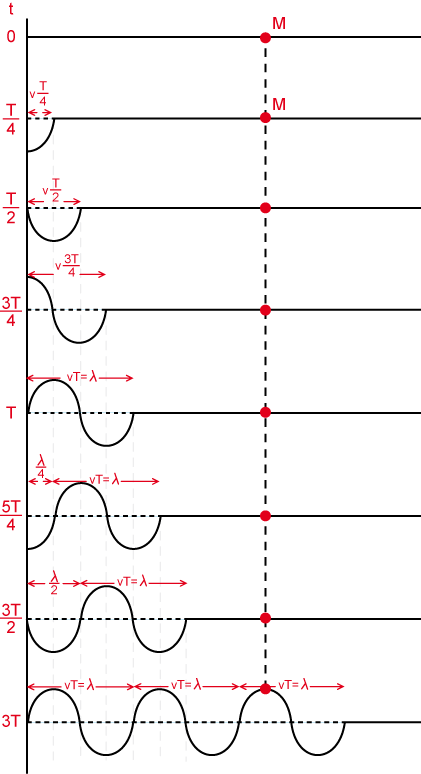
Observamos que cuando ha transcurrido un tiempo igual 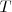 , en la cuerda se ha descrito una onda completa, el origen
, en la cuerda se ha descrito una onda completa, el origen 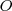 vuelve a vibrar entre
vuelve a vibrar entre 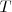 y
y 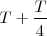 , del mismo modo que entre
, del mismo modo que entre  y
y  , luego cada nuevo periodo
, luego cada nuevo periodo 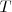 , un punto de la cuerda repite sus oscilaciones transversales. La onda es periódica en el tiempo.
, un punto de la cuerda repite sus oscilaciones transversales. La onda es periódica en el tiempo.
De igual modo, si nos movemos a lo largo de la cuerda, se observa que al avanzar segmentos de longitud 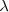 los puntos a esas distancias se mueven de igual modo, decimos que se encuentran en concordancia de fase o fase. La onda es periódica con relación al espacio.
los puntos a esas distancias se mueven de igual modo, decimos que se encuentran en concordancia de fase o fase. La onda es periódica con relación al espacio.
El movimiento tiene pues una doble periodicidad:
- - La onda es periódica en el tiempo, pues repite su vibración cada tiempo
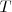 .
.
- - La onda es periódica en el espacio, pues repite su vibración cada distancia
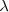 .
.
b) Ecuación de la onda
Si observamos el avance del tren de ondas, lo primero que destacamos es que el pulso inicial, tarda un tiempo 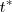 en alcanzar el punto
en alcanzar el punto 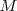 , el cual permanece en reposo en tanto que otros puntos ya han sido alcanzados por la perturbación.
, el cual permanece en reposo en tanto que otros puntos ya han sido alcanzados por la perturbación.
Ese tiempo 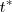 es tal que
es tal que 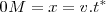 , con lo cual
, con lo cual 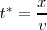
La ecuación de las oscilaciones del punto 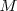 será igual a la del origen
será igual a la del origen 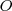 si a t le restamos el tiempo
si a t le restamos el tiempo 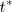 que el frente tarda en alcanzarlo. Podremos escribir:
que el frente tarda en alcanzarlo. Podremos escribir:
![y_M = A \mbox { } sen ( \omega [t - t^*]) = A \mbox { } sen (\omega [t - \frac{x}{v}]) y_M = A \mbox { } sen ( \omega [t - t^*]) = A \mbox { } sen (\omega [t - \frac{x}{v}])](/images/math/math-e156dd24021c029623969bf0e9731ffd.png)
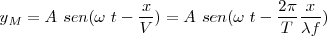
Pero 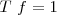 , con lo cual, la ecuación quedará:
, con lo cual, la ecuación quedará:
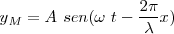
Pero si sustituimos 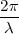 por
por 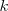 , la ecuación nos queda:
, la ecuación nos queda:
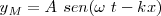
Del mismo modo que a 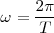 se le llama frecuencia angular o pulsación temporal a
se le llama frecuencia angular o pulsación temporal a 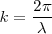 la llamamos pulsación espacial. Vemos que
la llamamos pulsación espacial. Vemos que 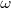 representa con relación a
representa con relación a  lo mismo
lo mismo 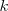 con relación a
con relación a  , como se puede ver en otra forma de escribir la ecuación
, como se puede ver en otra forma de escribir la ecuación
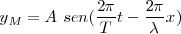
La ecuación tiene en cuenta la doble periodicidad del movimiento.
Para un instante  fijo, la ecuación nos indica cómo vibran las puntos del medio que se encuentren a una distancia variable x, y nos muestra que la función es periódica en el espacio.
fijo, la ecuación nos indica cómo vibran las puntos del medio que se encuentren a una distancia variable x, y nos muestra que la función es periódica en el espacio.
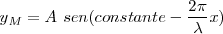
Pues puede observarse que para los puntos 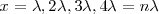 con
con 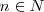 , presentan la misma la misma elongación y se encuentran vibrando del mismo modo, se encuentran en concordancia de fase o en fase. Nos muestra que la función es periódica en el espacio.
, presentan la misma la misma elongación y se encuentran vibrando del mismo modo, se encuentran en concordancia de fase o en fase. Nos muestra que la función es periódica en el espacio.
Si lo que mantenemos fijo es  , la ecuación nos indica cómo vibran los puntos situados a una distancia x, fija, en función del tiempo. Cada instante en el que el tiempo
, la ecuación nos indica cómo vibran los puntos situados a una distancia x, fija, en función del tiempo. Cada instante en el que el tiempo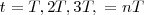 con
con 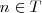 tiene la misma elongación y se encuentra vibrando de igual modo, la función es periódica en el tiempo:
tiene la misma elongación y se encuentra vibrando de igual modo, la función es periódica en el tiempo:
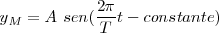
Si tenemos en cuenta la constante de fase que pueden presentar las oscilaciones del foco emisor, la ecuación se escribirá:
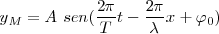
c) Fase
La fase de una onda es una magnitud escalar y se mide en radianes. La fase es una función del tiempo y de la abcisa x.
Si la ecuación de la onda es:
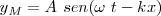
La fase viene dada por:
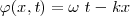
Esto nos conduce a decir que todos aquellos puntos (o superficies en las ondas tridimensionales) cuya fase tenga el mismo valor 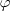 o
o 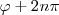 , con n numero entero. Los puntos se encuentran en concordancia de fase (o hablaremos de superficies equifásicas)
, con n numero entero. Los puntos se encuentran en concordancia de fase (o hablaremos de superficies equifásicas)
Pero del mismo modo podremos hablar de desfase o diferencia de fase.
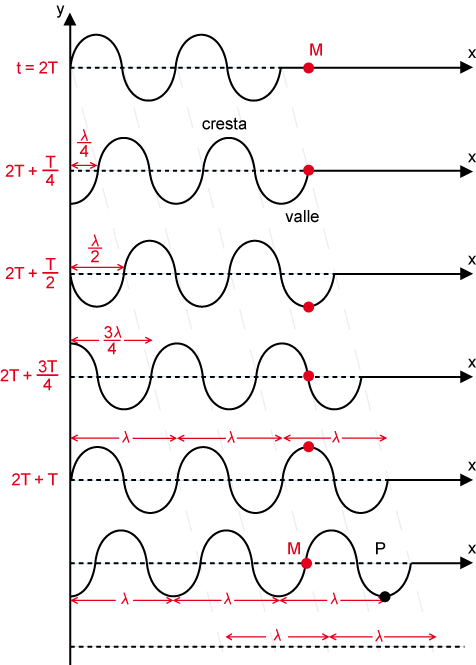
Siempre que, en un instante dado, el estado de vibración de un punto, por ejemplo, M, y de otro punto P sea diferente, hablaremos de un defase. La diferencia de fase nos vendrá dada por:
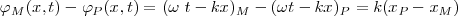
Casos particulares:
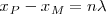 con
con 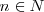 , los puntos se encuentran en fase o concordancia de fase.
, los puntos se encuentran en fase o concordancia de fase.
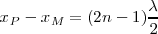 los puntos se encuentran en oposición de fase.
los puntos se encuentran en oposición de fase.
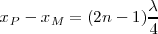 los puntos se encuentran en cuadratura con
los puntos se encuentran en cuadratura con  en avance sobre
en avance sobre 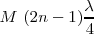
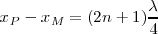 los puntos se encuentran en cuadratura con
los puntos se encuentran en cuadratura con  con retraso.
con retraso.