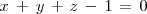Ecuaciones del plano
De Wikillerato
Un plano
 queda determinado cuando se conoce un punto
queda determinado cuando se conoce un punto
 del mismo y dos vectores
del mismo y dos vectores
 y
y
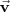 no nulos y linealmente independientes que éstan contenidos en el plano, llamados
vectores directores del plano.
no nulos y linealmente independientes que éstan contenidos en el plano, llamados
vectores directores del plano.
Existen diferentes formas de expresar la ecuación de un plano. Las describimos a continuación.
Tabla de contenidos[ocultar] |
Ecuación en forma vectorial
El plano
 que contiene al punto
que contiene al punto
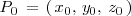 y tiene como vectores directores los vectores
y tiene como vectores directores los vectores
 y
y
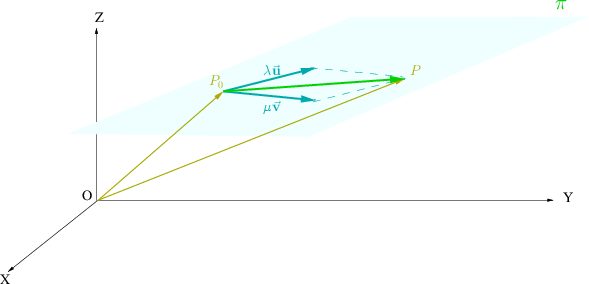
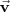 es el conjunto de puntos del espacio que verifican la siguiente relación vectorial:
es el conjunto de puntos del espacio que verifican la siguiente relación vectorial:
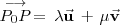
con
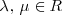
Teniendo en cuenta que
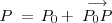 , resulta:
, resulta:
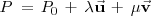
expresión que se conoce como ecuación vectorial del plano.
Ecuación en forma paramétrica
Desarrollando la ecuación vectorial expresada en componentes, resulta:
![\pi: \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x $ \, = \, x_0 \, + \, \mu v_x \, + \, \lambda u_x
\\
y $ \, = \, y_0 \, + \, \mu v_y \, + \, \lambda u_y
\\
z $ \, = \, z_0 \, + \, \mu v_z \, + \, \lambda u_z
\end{array}
</pre>
<p>\right.
\pi: \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x $ \, = \, x_0 \, + \, \mu v_x \, + \, \lambda u_x
\\
y $ \, = \, y_0 \, + \, \mu v_y \, + \, \lambda u_y
\\
z $ \, = \, z_0 \, + \, \mu v_z \, + \, \lambda u_z
\end{array}
</pre>
<p>\right.](/images/math/math-b3130c361706133daf92ba05b6195da8.png)
expresión que se conoce como ecuación en forma paramétrica.
Ecuación en forma general
Como
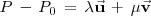
en el determinante
![\left|
</p>
<pre> \begin{array}[c]{rcl}
x \, - \, x_0 & u_x & v_x
\\
y \, - \, y_0 & u_y & v_y
\\
z \, - \, z_0 & u_z & v_z
\\
\end{array}
</pre>
<p>\right|
\left|
</p>
<pre> \begin{array}[c]{rcl}
x \, - \, x_0 & u_x & v_x
\\
y \, - \, y_0 & u_y & v_y
\\
z \, - \, z_0 & u_z & v_z
\\
\end{array}
</pre>
<p>\right|](/images/math/math-c30c90ef7b7dc0fa30e109f442074303.png)
la primera columna es combinación lineal de la segunda y de la tercera. Por tanto dicho
determinante es cero. Desarrollando el determinante, agrupando términos e igualando a 0,
nos queda un ecuación de la forma :
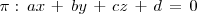
que es la ecuación en forma general, cartesiana o implícita del
plano. (
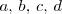 son números reales ).
son números reales ).
Ecuación normal
Otra forma de determinar la ecuación de un plano es conociendo un punto del mismo y un vector normal al plano.
Sea
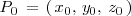 un punto dado del plano
un punto dado del plano
 y sea
y sea
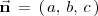 un vector normal a
un vector normal a
 . Entonces, para cualquier punto
. Entonces, para cualquier punto
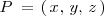 del plano
del plano
 , el vector
, el vector
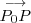 es perpendicular a
es perpendicular a
 , de manera que
, de manera que
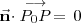
expresión que recibe el nombre de ecuación normal del plano. A partir de la ecuación normal del plano se puede obtener muy fácilmente su ecuación general:
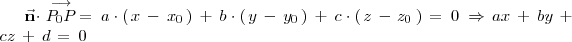
donde
 .
.
Ejemplo
Determinemos las ecuaciones del plano que contiene a los puntos:
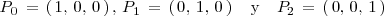
Tanto
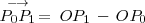
como
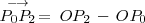
son vectores directores del plano
 , de manera que
, de manera que
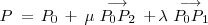
, es decir
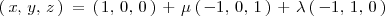
es la ecuación vectorial del plano
 . De la cual se deduce la ecuación de
. De la cual se deduce la ecuación de
 en forma paramétrica:
en forma paramétrica:
![\pi: \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x & = & 1 \, - \, \mu \, - \, \lambda
\\
y &= & \lambda
\\
z & = & \mu
\end{array}
</pre>
<p>\right.
\pi: \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x & = & 1 \, - \, \mu \, - \, \lambda
\\
y &= & \lambda
\\
z & = & \mu
\end{array}
</pre>
<p>\right.](/images/math/math-f8d38e83c2fb657edcafa1ebd7e83179.png)
Como
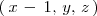 es una combinación lineal de
es una combinación lineal de
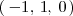 y de
y de
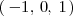 se ha de tener que
se ha de tener que
![\left|
</p>
<pre> \begin{array}[c]{ccc}
x \, - \, 1 & -1 & -1
\\
y & 1 & 0
\\
z & 0 & 1
\\
\end{array}
</pre>
<p>\right|
\, = \, 0
\left|
</p>
<pre> \begin{array}[c]{ccc}
x \, - \, 1 & -1 & -1
\\
y & 1 & 0
\\
z & 0 & 1
\\
\end{array}
</pre>
<p>\right|
\, = \, 0](/images/math/math-da1c38299a6454d12bf1200af9e0318e.png)
de lo que se deduce la ecuación de
 en forma general, cartesiana o implícita:
en forma general, cartesiana o implícita: