La cantidad de movimiento
De Wikillerato
Cuando se estudia la cinemática, el movimiento de un cuerpo viene definido por su velocidad. Al estudiar la dinámica interviene también la masa. La cantidad de movimiento es una magnitud física que liga la masa y la velocidad de un móvil. Al igual que la velocidad, esta magnitud puede variar cuando se ejerce una fuerza sobre un sistema. Es el caso del lanzamiento de un proyectil, aun cuando las deformaciones del sistema sean un tanto complejas. Cuando un cañón dispara un obús, la duración de la fuerza aplicada es muy corta. El proyectil adquiere una velocidad y continúa su camino siguiendo una trayectoria parabólica. Por su parte, el cañón retrocede y es sujetado por un sistema de cuerdas. Si se lanza un proyectil con una escopeta es el hombro el que soporta la fuerza ejercida por la culada en su retroceso. Pero se pueden poner ejemplos más simples, como el movimiento de un ciclista, del cual se pueden calcular tanto su centro de inercia como su cantidad de movimiento. También en el juego de billar, se da un impulso a una bola blanca con el taco, la bola choca con la roja, a la cual aporta una cierta cantidad de movimiento y se modifica el que tenía la bola blanca antes del choque.
Tabla de contenidos[ocultar] |
El vector cantidad de movimiento
Si en una pista de patinaje, dos patinadores juegan a lanzarse un balón en una dirección sensiblemente horizontal , se puede observar :
El patinador B, inmóvil, recibe la pelota con una velocidad 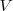 , al recogerla, observamos que retrocede con una velocidad
, al recogerla, observamos que retrocede con una velocidad 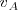 con la misma dirección y sentido que
con la misma dirección y sentido que 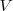 , pero cuyo módulo es bastante menor que el de la pelota
, pero cuyo módulo es bastante menor que el de la pelota 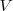 . Simultáneamente, el patinador B, en el instante que lanza la pelota también retrocede con una velocidad
. Simultáneamente, el patinador B, en el instante que lanza la pelota también retrocede con una velocidad 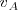 en la misma dirección que
en la misma dirección que 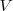 , pero con sentido contrario y cuyo módulo es menor que el de la velocidad de la pelota
, pero con sentido contrario y cuyo módulo es menor que el de la velocidad de la pelota 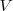 .
.
Al producto de la masa por la velocidad se le llama vector cantidad de movimiento  de modo que
de modo que 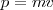 .
.
Teniendo en cuenta que la masa es una magnitud escalar y siempre 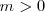 , el vector cantidad de movimiento
, el vector cantidad de movimiento  tendrá l misma dirección y sentido que
tendrá l misma dirección y sentido que  y su módulo igual
y su módulo igual 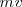 .
.
Las unidades en que debe expresarse son 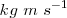 .
.
Cantidad de movimiento de un sólido
Cuando se trata de un sólido rígido, su vector cantidad de movimiento será la suma de los infinitos vectores 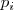 de cada partícula de las que componen el sistema
de cada partícula de las que componen el sistema
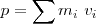 de donde
de donde 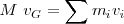
Con lo cual 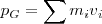
Conservación de la cantidad de movimiento de un sistema
Puede hacerse en el laboratorio una sencilla experiencia.
Sobre un carril, colocamos dos carritos de igual masa. Intercalamos entre ambos un resorte comprimido y sujetamos los carritos mediante un hilo de nylon Si en un instante dado quemamos el hilo de nylon, los carritos salen despedidos impulsados por la fuerza recuperadora del resorte. Si ambos carritos tienen igual forma e igual masa, la experiencia nos muestra que el módulo de las velocidades que adquieren ambos carritos son iguales, pero de sentido contrario. Teniendo en cuenta que la masa de los carritos es muy pequeña y que el coeficiente de rozamiento de rodadura también lo es, el movimiento de los carritos será rectilíneo y uniforme y colineal pero de sentido opuesto. La suma de los vectores velocidad es cero
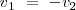 , dado que las masas de los carritos son iguales
, dado que las masas de los carritos son iguales 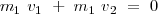 ,
, 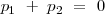
Pero la cantidad de movimiento del sistema antes de quemar el hilo de nylon es cero pues su velocidad es cero.
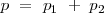
En ausencia de fuerzas exteriores la cantidad de movimiento permanece constante.
Si añadimos una masa a uno de los carritos,de tal modo que 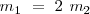
Dado que la cantidad de movimiento inicial del sistema es cero
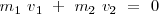 ,
, 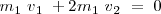 ;
; 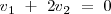 ;
; 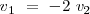
Si 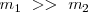 entonces
entonces 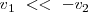 es el caso de los lanzamientos de obuses, el obús sale veloz y el cañón retrocede a una velocidad mucho menor.
es el caso de los lanzamientos de obuses, el obús sale veloz y el cañón retrocede a una velocidad mucho menor.
Choques
Choques inelásticos
Pero al igual que se conserva la cantidad de movimiento cuando un sistema se desgaja podemos decir lo mismo cuando tiene lugar un choque totalmente inelástico, en cuyo caso las dos masas que se encuentran salen formando un sólo cuerpo.
Imaginemos un carrito que soporta un placa de plomo en posición vertical cuya masa es m2. Con una escopeta de aire comprimido se dispara un plomillo sobre la placa, de modo que queda incrustado en la placa.
La cantidad de movimiento inicial del carrito es cero pues su velocidad es cero. Sin embargo el plomillo lleva una velocidad v, y su cantidad de movimiento es 
La cantidad de movimiento total del sistema es 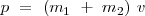 , siendo v la velocidad del sistema después del choque. Tenemos que
, siendo v la velocidad del sistema después del choque. Tenemos que
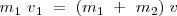
con lo cual 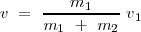
Si, como en uno de los ejemplos expuestos, 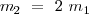
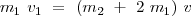 , con lo cual
, con lo cual 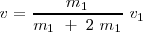
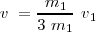 nos queda
nos queda
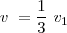
Choques elásticos
Recuperemos el juego de billar.
 antes del choque =
antes del choque = 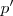 después del choque
después del choque
Si consideramos que la bola roja se encuentrea en reposo antes del choque
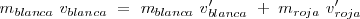
De un modo general , dados dos sólidos, 1 y 2, en movimiento que realizan un choque perfectamente elástico
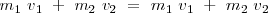
Propulsión a reacción
Es el principio de los aviones a reacción o del lanzamiento de los cuerpos al espacio.
El combustibles expulsa gases de una cierta masa m hacia atrás con una cierta velocidad 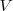 , medida con relación al avión o a la nave espacial. La masa restante,
, medida con relación al avión o a la nave espacial. La masa restante,  , es necesariamente propulsada hacia adelante con una velocidad
, es necesariamente propulsada hacia adelante con una velocidad  .
.
El vector cantidad de movimiento del sistema debe permanecer nulo.
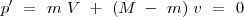
con lo cual