Método general de la ciencia: definición, división y demostración
De Wikillerato
Tabla de contenidos[ocultar] |
La definición
Definir significa poner límites; cuando definimos respondemos a la pregunta: ¿Qué es? En toda definición se distingue el definiendum y el definiens, es decir lo que se ha de definir y lo que se define. Si digo: “El cuadrilátero es un polígono de cuatro lados” , cuadrilátero es el definiendum y polígono de cuatro lados el definiens.
Clases de definición
- La sinonímica explica el significado del nombre recurriendo a otra palabra que signifique lo mismo, a un sinónimo. Por ejemplo, el cloruro sódico es la sal común.
- La etimológica explica el significado del nombre recurriendo al origen del mismo. Por ejemplo, nombre viene del latín “nomen”.</li>
- Esencial. Se hace por el género próximo y la diferencia específica. El género próximo es aquella característica que de modo inmediato tiene el objeto a definir con otros objetos de especies diferentes. En el ejemplo anterior, polígono es el género al que pertenece el cuadrilátero. La diferencia específica es la característica que distingue al objeto que se quiere definir de otros objetos que pertenecen al mismo género. En el caso del cuadrilátero la diferencia es tener cuatro lados, característica que le distingue de otros polígonos como el triángulo o el pentágono.
- Definición descriptiva por una propiedad. La propiedad es la característica que poseen todos los miembros de una especie, como la capacidad de reír en el ser humano, y no por ejemplo el hecho de ser vivo que comparte con los animales y las plantas.
- Descriptiva por un conjunto de características que no son ni el género próximo ni la diferencia específica. El mejor ejemplo de este tipo de definición, lo puso Platón cuando dijo que el ser humano es “bípedo implume”.
- Genética. Nos dice cómo se produce el objeto a definir. Por ejemplo: “El bronce se forma con la mezcla de cobre y zinc”.
- Causal. Indica una de las causas productoras del objeto: Causa final, expresa el objetivo o fin al que se destina el objeto. Un pupitre es una mesa para escribir en el colegio. Causa eficiente, dice lo que produce o da existencia al objeto: el carpintero o la industria fabricadora del pupitre. Causa ejemplar, señala el modelo o patrón según el que se ha fabricado el objeto: los pupitres se han fabricado siguiendo el modelo oficial del Ministerio o Comunidad Autónoma.
- Operacional: Expresa un procedimiento experimental capaz de ser operado, de ser construido o manipulado. “Ácido es aquella sustancia que enrojece el papel de tornasol”.
- Recursiva: Se define el objeto en relación con uno o más términos de una secuencia numerable. En Astronomía se suele definir la luminosidad de las estrellas mediante una fórmula de recurrencia. Por ejemplo,
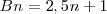 . En esta fórmula B es la luminosidad, n la magnitud de la estrella; la luminosidad de la estrella es 2,5 veces la de una estrella de magnitud 4.
. En esta fórmula B es la luminosidad, n la magnitud de la estrella; la luminosidad de la estrella es 2,5 veces la de una estrella de magnitud 4.
Leyes de la definición
La lógica nos da una serie de leyes para que la definición sea correcta.
- El definiens debe ser más claro que el definiendum. De esta ley se deducen otras subleyes:
- El definiendum no debe formar parte del definiens.
- El definiens debe ser breve ya que una definición larga suele ser oscura y confusa.
- El definiens no debe ser negativo. Sólo hay una excepción en que sí puede ser válida, y es cuando definimos una falta o privación, por ejemplo: “Ciego es una persona que no puede ver”.
- El definiens debe convenir a todo el definiendum y sólo a él. De aquí se derivan:
- El definiens no debe ser más estricto que el definiendum.
- El definiens no debe ser más amplio que el definiendum.
La definición bien hecha es clave en la ciencia, porque necesita aclarar los conceptos que maneja para dar una explicación correcta del objeto de su estudio.
Sin embargo, la definición tiene sus límites. Bertrand Russell decía:”Puesto que todos los términos que se definen, son definidos mediante otros término, es evidente que el conocimiento humano debe siempre contentarse con aceptar algunos términos como “inteligibles” sin definición con el fin de tener un punto de partida para sus definiciones”.
Existen, pues, los llamados indefinibles, conceptos que se escapan de la definición como los axiomas matemáticos, o conceptos relativos a la experiencia, tales como el dolor, la locura, el enamoramiento etc.
Ejercicios
Construir definiciones por género y especie de los siguientes términos:
- Compositor
- Poeta
- Elemento
- Flor
- General
- Inventora
- Científica
Criticar positiva o negativamente las siguientes definiciones indicando a qué clase corresponden:
- “Cuadrado es una figura plana formada por dos triángulos isósceles que tienen una hipotenusa en común “.
- “Fragancia significa cualquier olor”.
- “Honestidad significa ausencia habitual del intento de engañar”.
- “Libertad es la capacidad humana de elegir libremente entre dos o más alternativas o posibilidades genuinas; elección que está siempre limitada por el pasado y las circunstancias del presente inmediato”.
- “La palabra cuerpo significa aquello que llena u ocupa cierto espacio o lugar imaginado, y no depende de la imaginación, sino que forma parte real de lo que llamamos el universo” (Hobbes, Thomas Leviatán).
- “Un cínico es una persona que conoce el precio de todo y el valor de nada”(Oscar Wilde El abanico de Lady Windermere).
La división
Es la operación que consiste en dividir un todo en sus partes. En este proceso de la división distinguimos:
- El todo que se divide.
- Las partes resultantes.
- El fundamento o criterio de la división, es decir, el punto de vista desde el que dividimos. Por ejemplo, una familia se puede dividir en padres e hijos, pero desde el punto de vista social en: matriarcal, endogámica, patriarcal etc.
Clases de división
- Física: El todo que se divide es físico, en el que sus partes son distintas entre sí. La división física puede ser a su vez:
- Física cuantitativa: Un todo se divide en sus partes homogéneas, como un pastel en trozos.
- Física esencial: Aquí se divide un todo en sus componentes esencial, el agua se divide en hidrógeno y oxígeno.
- Física accidental: Un todo se divide en los componentes que lo constituyen como un agregado, por ejemplo, separar las piezas de un puzzle.
- Lógica: Las partes se distinguen por la razón humana. La animalidad y la racionalidad en el ser humano.
- Moral:El todo a dividir es un todo moral, cuyas partes se distinguen pero permanecen unidas por un vínculo moral. En el ejercicio de la justicia, distinguimos jueces y letrados, con funciones distintas, pero ambos sirven a la justicia.
Leyes de la división
- Ha de ser completa, es decir, ha de expresar todas las partes posibles de manera que la suma de las partes sea igual al todo.
- Las partes deben ser irreductibles entre sí. Cada parte ha de excluir a las demás.
- El fundamento o criterio de la división no debe cambiarse en el proceso de la misma.
La división es un medio eficaz para realizar las explicaciones científicas. Descartes, el gran filósofo racionalista francés dio a la división – que él llamó análisis- una gran importancia como parte insustituible del método universal. En el Discurso del método y en Las Reglas para dirigir el espíritu, el análisis es el segundo paso de ese método por él diseñado para no caer en el error y alcanzar la verdad: “Dividir cada una de las dificultades que examinase en cuantas partes fuese posible y en cuantas requiriese su mejor solución”.
Sólo dividiendo los problemas en sus partes más pequeñas, se podrán investigar y resolver.
La demostración
Aristóteles en su obra sobre la lógica, Organon, definió la demostración como “un razonamiento en el que, partiendo de premisas verdaderas, se llega a una conclusión verdadera que se deriva necesariamente de las premisas”. Distinguió a la demostración del razonamiento sofístico, en el que al menos una de sus premisas es falsa, del posible o dialéctico, en el que al menos una de sus premisas es posible.
Clases de demostración
- A priori y a posteriori. La demostración a priori se basa en la causa para demostrar el efecto: Si Picasso es un gran pintor (causa), el Guernica es un buen cuadro (efecto). En la demostración a posteriori vamos de los efectos a las causas: Por los destrozos ocasionados, la fuerza del huracán ha sido terrible.
- Racional y experimental. La demostración racional (propter quid en latín), se basa en la especulación exclusivamente racional, como en las demostraciones matemáticas. La demostración experimental (quia), se funda en datos experimentales como las demostraciones en Química.
- Directa e indirecta. En la demostración directa, se parte de las premisas y se alcanza la conclusión. En la indirecta, llamada también reducción al absurdo, se trata de demostrar la negación de la tesis que hemos sometido a demostración, demostrando que si admitimos tal negación se llega a un absurdo o contradicción, con lo que indirectamente se demuestra la proposición inicial, un buen ejemplo de demostración indirecta se encuentra en el método de invalidez formal en la lógica proposicional.
- Demostración absoluta ad veritatem y demostración ad hominem”. La demostración absoluta es válida para cualquier inteligencia, como el teorema de Pitágoras. En la demostración ad hominem, se parte de una proposición admitida por la persona a la que se le quiere demostrar una tesis, aunque esa proposición sea discutible o falsa, para hacerle llegar a la conclusión contraria a la que mantenía. Es el tipo de argumento que se maneja contra los escépticos que afirman "no estar seguros de ninguna proposición", entonces se les argumenta: “¿Estáis seguros de la anterior proposición?, Si es así, esto contradice lo que afirmáis.”
- Analítica y sintética. En la analítica se procede pasando de lo complejo a lo simple. En la electrolisis el agua se descompone en oxígeno e hidrógeno. En la sintética, el proceso es inverso: verificar el agua a partir del hidrógeno y el oxígeno.
Después de conocer todas las formas de demostración, podemos preguntarnos si puede demostrarse todo. Para demostrar una proposición, partimos de unas premisas verdaderas que a su vez se apoyan en otras ya demostradas y así sucesivamente, pero no podemos caer en una cadena infinita de demostraciones, por lo que hemos de admitir unos primeros principios indemostrables.
Principios indemostrables
Estos primeros principios deben ser evidentes, es decir poseer tal transparencia y claridad que los admitamos inmediatamente como verdaderos, por ejemplo el principio de identidad: “Una cosa es igual a sí misma”, o el de contradicción: “Una proposición y su negación no pueden ser a la vez verdadera y falsa”.
Hoy en día, sin embargo, los lógicos de la ciencia no establecen estos primeros principios como evidentes, sino como proposiciones cuya verdad se admite sin más, como axiomas.
Este fenómeno se ha producido al haberse comprobado los fallos en la evidencia de algunos primeros principios como “el todo es mayor que la parte”. Un ejemplo lo brinda la matemática, donde el conjunto de los números pares es igual al de los números naturales, siendo el primero una parte del segundo.



