Buscar en WikilleratO
Temario:
Seleccionar asignatura
Matemáticas
Física
Filosofía
Lengua y Literatura
Dibujo Técnico
Historia
Historia del Arte
Química
Biología
Dependencia e independencia lineal
De Wikillerato
(Diferencias entre revisiones)
m
Línea 45:
Línea 45: <br/>
<br/>
-
- ==Independencia lineal==
-
- <br/>
-
- Los vectores
- <math>
- \vec{\mathbf{v}}_1, \, \vec{\mathbf{v}}_2, \, \ldots, \, \vec{\mathbf{v}}_n
- </math>
- son linealmente independientes si:
-
- <br/>
-
- <center>
- <math>
- \alpha_1 \vec{\mathbf{v}}_1 \, + \, \alpha_2 \vec{\mathbf{v}}_2 \, + \, \ldots \, + \,
- \alpha_n \vec{\mathbf{v}}_n \, = \, 0 \, \Rightarrow \, \alpha_1 \, = \, \alpha_2 \, = \,
- \ldots \, = \, \alpha_n \, = \, \ldots \, = \, 0
- </math>
- </center>
-
- <br/>
-
- ===Ejemplo===
-
- <br/>
-
- Los vectores
- <math>
- \vec{\mathbf{u}} \, = \,
- \left(
- \, 1, \, 0, \, 1 \,
- \right)
- , \,
- \vec{\mathbf{v}} \, = \,
- \left(
- \, 0, \, 1, \, 0 \,
- \right)
- </math>
- y
- <math>
- \vec{\mathbf{w}} \, = \,
- \left(
- \, 0, \, 0, \, 1 \,
- \right)
- </math>
- son linealmente independientes, pues:
-
- <br/>
-
- <center>
- <math>
- \alpha \vec{\mathbf{u}} \, + \, \beta \vec{\mathbf{v}} \, + \, \ldots \, + \,
- \gamma \vec{\mathbf{w}} \, = \, 0 \, \Rightarrow
- </math>
- <math>
- \left(
- \, \alpha, \, 0, \, \alpha \,
- \right)
- \, + \,
- \left(
- \, 0, \, \beta, \, 0 \,
- \right)
- \, + \,
- \left(
- \, 0, \, 0, \, \gamma \,
- \right)
- \, = \,
- \left(
- \, \alpha, \, \beta, \, \alpha \, + \, \gamma \,
- \right)
- \, = \,
- </math>
-
- <br/>
-
- <math>
- \, = \,
- \left(
- \, 0, \, 0, \, 0 \,
- \right)
- \, \Rightarrow \, \alpha \, = \, \beta \, = \, \gamma \, = \, 0
- </math>
- </center>
-
- <br/>
-
- ----
-
- <br/>
-
- Los vectores
- <math>
- \vec{\mathbf{v}}_1, \, \vec{\mathbf{v}}_2, \, \ldots, \, \vec{\mathbf{v}}_n
- </math>
- son linealmente dependientes si existen numeros reales
- <math>
- \alpha_1, \, \alpha_2, \, \ldots \, , \, \alpha_n
- </math>
- no todos nulos tales que:
-
- <br/>
-
- <center>
- <math>
- \alpha_1 \vec{\mathbf{v}}_1 \, + \, \alpha_2 \vec{\mathbf{v}}_2 \, + \, \ldots \, + \,
- \alpha_n \vec{\mathbf{v}}_n \, = \, 0
- </math>
- </center>
-
- <br/>
-
- ===Ejemplo===
-
- <br/>
-
- Los vectores
- <math>
- \vec{\mathbf{u}} \, = \,
- \left(
- \, 1, \, 0, \, 1 \,
- \right)
- , \,
- \vec{\mathbf{v}} \, = \,
- \left(
- \, -1, \, 1, \, 0 \,
- \right)
- </math>
- y
- <math>
- \vec{\mathbf{w}} \, = \,
- \left(
- \, 1, \, 1, \, 2 \,
- \right)
- </math>
- son linealmente dependientes, pues:
-
- <br/>
-
- <center>
- <math>
- \alpha \vec{\mathbf{u}} \, + \, \beta \vec{\mathbf{v}} \, + \, \ldots \, + \,
- \gamma \vec{\mathbf{w}} \, = \, 0 \, \Rightarrow
- </math>
-
- <br/>
-
- <math>
- \left(
- \, \alpha \, - \, \beta \, + \, \gamma, \, \beta \, + \, \gamma, \, \alpha \, + \, 2\gamma \,
- \right)
- \, = \,
- \left(
- \, 0, \, 0, \, 0 \,
- \right)
- </math>
- </center>
-
- <br/>
-
- Igualando componentes:
-
- <br/>
-
- <center>
- <math>
- \left.
- \begin{array}[c]{rcl}
- \alpha\, - \, \beta \, + \, \gamma & = & 0
- \\
- \beta \, + \, \gamma & = & 0
- \\
- \alpha \, + \, 2\gamma & = & 0
- \end{array}
- \right\}
- \, \Rightarrow \beta \, = \, -\gamma, \, \alpha \, = \, -2\gamma
- </math>
- </center>
-
- <br/>
-
- Para cualquier valor que tome
- <math>
- \gamma \neq 0
- </math>
- se obtiene un valor para
- <math>
- \beta
- </math>
- y otro para
- <math>
- \alpha
- </math>
- tambien distintos de cero, luego
- <math>
- \vec{\mathbf{u}}
- </math>
- ,
- <math>
- \vec{\mathbf{v}}
- </math>
- y
- <math>
- \vec{\mathbf{w}}
- </math>
- son linealmente dependientes.
-
- <br/>
-
- ----
-
- <br/>
-
- En
- <math>
- R^2
- </math>
- , dos vectores
- <math>
- \vec{\mathbf{u}} \, = \,
- \left(
- \, u_1, \, u_2 \,
- \right)
- </math>
- y
- <math>
- \vec{\mathbf{v}} \, = \,
- \left(
- \, v_1, \, v_2 \,
- \right)
- </math>
- son:
-
- <br/>
-
- <center>
- <table
- border = "n" >
- <tr>
- <td>
- linealmente <span style= 'color:#00AA00'> independientes
- </span> si:
- </td>
- <td>
- linealmente <span style= 'color:#00AA00'> dependientes
- </span> si:
- </td>
- </tr>
- <tr>
- <td>
- <center>
- [[Imagen:determinante.gif]]
- </center>
- </td>
- <td>
- <center>
- [[Imagen:determinante2.gif]]
- </center>
- </td>
- </tr>
- </table>
- </center>
-
- <br/>
-
- En
- <math>
- R^3
- </math>
- , tres vectores
- <math>
- \vec{\mathbf{u}} \, = \,
- \left(
- \, u_1, \, u_2, \, u_3 \,
- \right)
- </math>
- ,
- <math>
- \vec{\mathbf{v}} \, = \,
- \left(
- \, v_1, \, v_2, \, v_3 \,
- \right)
- </math>
- y
- <math>
- \vec{\mathbf{w}} \, = \,
- \left(
- \, w_1, \, w_2, \, w_3 \,
- \right)
- </math> son:
-
- <br/>
-
- <center>
- <table
- border = "n" >
- <tr>
- <td>
- linealmente <span style= 'color:#00AA00'> independientes </span> si:
- </td>
- <td>
- linealmente <span style= 'color:#00AA00'> dependientes </span> si:
- </td>
- </tr>
- <tr>
- <td>
- <center>
- [[Imagen:determinante3.gif]]
- </center>
- </td>
- <td>
- <center>
- [[Imagen:determinante4.gif]]
- </center>
- </td>
- </tr>
- </table>
- </center>
-
- <br/>
-
- [[Categoría:Matemáticas]]
Revisión de 23:53 28 sep 2009
Combinación lineal
Una combinación lineal de los vectores
siendo los coeficientes
Ejemplo
Dados los vectores
Los contenidos de
Wikillerato están disponibles bajo una
licencia de Creative Commons .
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.
 , es una suma de la forma:
, es una suma de la forma:
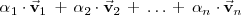
 numeros reales.
numeros reales.
 y
y
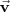 , una combinación lineal de ellos es el vector
, una combinación lineal de ellos es el vector