Significado geométrico de la derivada
De Wikillerato
m (Revertidas las ediciones realizadas por 190.43.246.80 (Talk); a la última edición de Fjmolina) |
|||
| Línea 18: | Línea 18: | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | . | + | . Supongamos que todos estos puntos estan a la derecha de |
<math> | <math> | ||
A | A | ||
Revisión de 08:17 8 feb 2010
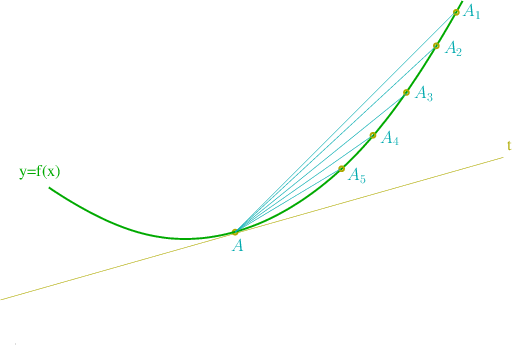
Consideremos la grafica de una función
 . Tomemos un punto
. Tomemos un punto
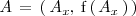 en dicha grafica y consideremos una sucesión de puntos
en dicha grafica y consideremos una sucesión de puntos
 en la grafica de
en la grafica de
 . Supongamos que todos estos puntos estan a la derecha de
. Supongamos que todos estos puntos estan a la derecha de
 y que cuando
y que cuando
 ,
,
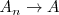 .
.
La recta que pasa por los puntos
 y
y
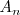 es una secante a la grafica de la función
es una secante a la grafica de la función
 . De esta forma, hay una secante para cada punto
. De esta forma, hay una secante para cada punto
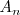 . Sea
. Sea
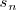 la recta que pasa por
la recta que pasa por
 y por
y por
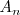 .
.
Cuando
 tiende a
tiende a
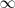 ,
,
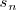 tiende a la tangente a la grafica de la función
tiende a la tangente a la grafica de la función
 en el punto
en el punto
 ,
,
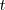 :
:
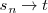
Habria de esperar, pues, que la pendiente de
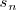 tienda a la pendiente de
tienda a la pendiente de
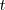 cuando
cuando
 tiende a
tiende a
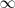 . Como la pendiente de
. Como la pendiente de
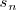 es una tasa de variación
media:
es una tasa de variación
media:
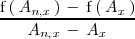
(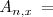 abcisa de
abcisa de
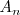 )
)
su limite cuando
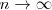 es una tasa de variación instantánea, la derivada de
es una tasa de variación instantánea, la derivada de
 en
en
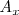 ; es decir la pendiente de
; es decir la pendiente de
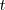 es la derivada de
es la derivada de
 en
en
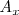 .
.