Áreas de triángulos y tetraedros
De Wikillerato
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| - | =Área de un triángulo del que se conocen los vertices | + | ==Área de un triángulo del que se conocen los vertices== |
<br/> | <br/> | ||
| Línea 12: | Línea 12: | ||
\mathbf{v} | \mathbf{v} | ||
</math> | </math> | ||
| - | + | ||
<br/> | <br/> | ||
| Línea 28: | Línea 28: | ||
<br/> | <br/> | ||
| - | El área de un triágulo es la mitad del área del paralelogramo | + | El área de un triágulo |
| - | + | ||
| + | <br/> | ||
| + | |||
| + | [[Imagen:paralelogramoYTrigb.png]] | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | es la mitad del área del paralelogramo determinado por los vectores | ||
<math> | <math> | ||
| - | \text{Area del \overset{\triangle}{ABC | + | \Vec{AB} |
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | \vec{AC} | ||
| + | <math>: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | <center> | ||
| + | \text{Area del} \overset{\triangle}{ABC} = \frac{1}{2} \cdot \left| \, \Vec{AB} \times \vec{AC} \, \right| | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 84: | Línea 102: | ||
por | por | ||
<math> | <math> | ||
| - | \ | + | \Vec{AB} |
</math>, | </math>, | ||
<math> | <math> | ||
Revisión de 10:37 7 nov 2010
Área de un triángulo del que se conocen los vertices
El área de un paralelogramo determinado por dos vectores
 y
y

es el módulo de su producto vectorial:
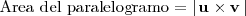
El área de un triágulo
es la mitad del área del paralelogramo determinado por los vectores
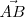 y
y
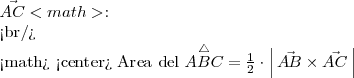 </center>
</center>
Volumen de un tetraedro del que se conocen los vértices
El volumen del paralepípedo determinado por tres vectores
 .
.
 y
y
 es el valor absoluto del producto mixto de esos vectores:
es el valor absoluto del producto mixto de esos vectores:
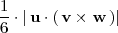
El volumen de un tetraedro determinado por
 .
.
 y
y
 es:
es:
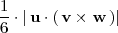
En caso, de que conociesemos los vertices A, B, C y D del tetraedro, podriamos
utilizar la formula anterior remplazando
 por
por
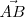 ,
,
 por
por
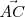 ,
y
,
y
 por
por
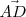 .
.