Concepto de velocidad

De Wikillerato

(Diferencias entre revisiones)

Saltar a navegación, búsqueda

Revisión de 16:06 4 dic 2006

Velocidad media

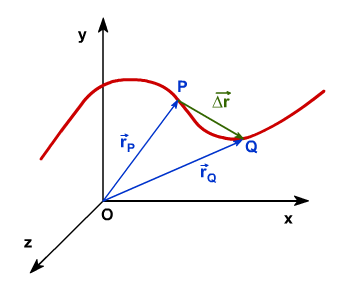
La velocidad se puede se puede definir como la variación temporal de la posición del punto material

$\vec v = \frac{ \Delta \vec r}{ \Delta t } = \frac { \vec r_Q - \vec r_P }{\Delta t }$

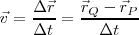
Este cociente nos define lo que llamamos velocidad media. Si consideramos que

$\vec r = r_x\vec i + r_y\vec j + r_z \vec k$

$\vec v= \frac{\Delta \vec r}{\Delta t } = \frac {\Delta r_x}{ \Delta t }\vec i + \frac{\Delta r_y}{ \Delta t }\vec j + \frac{\Delta r_z}{ \Delta t }\vec k$

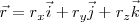
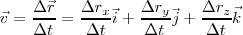
Si pretendemos calcular la velocidad entre dos instantes definidos por 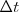$\Delta t$ , obtenemos:

$\vec v = \frac { \vec r (t + \Delta t) - \vec r (t)}{ \Delta t}$

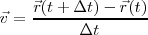
Velocidad instantánea

Hemos definido la velocidad media, y la hemos definido intuitivamente. Hemos trazado el vector que va desde la posición inicial a la posición final, cuya dirección siempre coincide con la cuerda que une esos dos puntos. Si hacemos cada vez más breves los intervalos de tiempo, la dirección de las cuerdas, y en consecuencia las de los vectores desplazamiento, se van aproximando a la dirección de la tangente a la trayectoria. Si pretendemos determinar la velocidad del móvil en un instante preciso, que denominaremos velocidad instantánea en el instante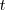 $t$ , observamos que su dirección coincidirá con la de la tangente a la trayectoria en cada instante.

Y podremos calcular la velocidad en un instante t:

$\vec v= \lim_{\Delta t\to 0} \frac{\Delta \vec r }{\Delta t } = \lim_{\Delta t\to 0} \frac {\Delta r_x }{\Delta t}\vec i + \lim_{\Delta t\to 0} \frac {\Delta r_y }{\Delta t}\vec j + \lim_{\Delta t\to 0} \frac {\Delta r_z }{\Delta t}\vec k$

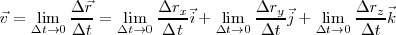
y en consecuencia:

$\vec v = \frac{ d \vec r}{ dt } = \frac{d r_x}{ dt }\vec i + \frac {d r_y}{ dt } \vec j + \frac {d r_z}{ dt }\vec k$

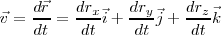
o lo que es igual :

$\vec v = v_x\vec i + v_y\vec j + v_z\vec k$

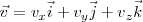
La velocidad instantánea es una magnitud vectorial cuya dirección coincide siempre con la de la tangente a la trayectoria y su sentido el del movimiento. Al módulo se le llama rapidez, que es una magnitud escalar.

Obtenido de "http://wikillerato.org/Concepto_de_velocidad.html"

Categoría: Física