Navegación
Sistema diédrico
De Wikillerato
| Línea 18: | Línea 18: | ||
===Resolución de problemas=== | ===Resolución de problemas=== | ||
Se trata de resolver problemas básicos de representación, distancias, paralelismo, perpendicularidad, ángulos, intersecciones con rectas y planos y desarrollos. | Se trata de resolver problemas básicos de representación, distancias, paralelismo, perpendicularidad, ángulos, intersecciones con rectas y planos y desarrollos. | ||
| + | |||
| + | ==Enlaces Externos== | ||
| + | |||
| + | {{Problemas}} | ||
| + | |||
[[Categoría:Dibujo]] | [[Categoría:Dibujo]] | ||
Revisión de 15:07 8 sep 2008
Uno o más usuarios están trabajando actualmente en extender este artículo.
Es posible que, a causa de ello, haya lagunas de contenido o deficiencias de formato. Por favor, antes de realizar correcciones mayores o reescrituras, contacta con ellos en la página de discusión.
Tabla de contenidos |
Fundamento del sistema
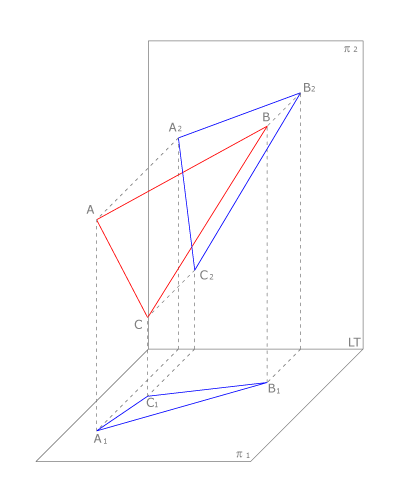
Está basado en la proyección cilíndrica ortogonal de los objetos sobre dos planos de proyección que forman un diedro rectangular.
En la figura vemos un triángulo 
que se proyecta sobre el plano vertical como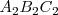 
y sobre el plano horizontal como 
.
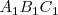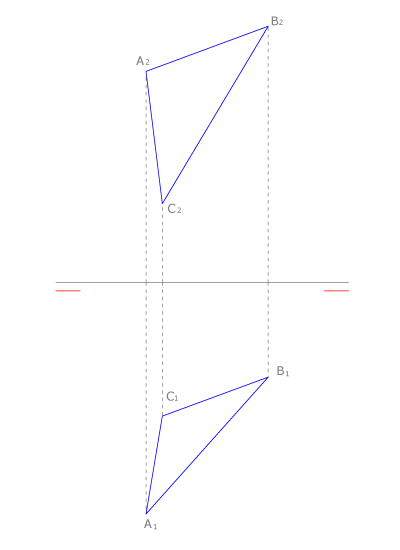
La representación diédrica sobre un plano se logra abatiendo el plano horizontal sobre el vertical como vemos en la figura.
Métodos operativos
Son los métodos geométricos que aplicaremos a las características del sistema diédrico.
Resolución de problemas
Se trata de resolver problemas básicos de representación, distancias, paralelismo, perpendicularidad, ángulos, intersecciones con rectas y planos y desarrollos.
Enlaces Externos
También te pueden interesar los siguientes ejercicios resueltos de selectividad
