Funciones acotadas
De Wikillerato
| Línea 1: | Línea 1: | ||
<br/> | <br/> | ||
| - | ==Definición== | + | ==Definición de dominio== |
<br/> | <br/> | ||
| - | + | En principio y hablando con rigor, el dominio de una función es parte de la definición de esa | |
| - | + | función. | |
| - | + | ||
| - | + | ||
| - | de | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
==Ejemplo== | ==Ejemplo== | ||
| Línea 44: | Línea 14: | ||
<br/> | <br/> | ||
| - | + | Las funciones | |
<center> | <center> | ||
<math> | <math> | ||
| - | \left[ \, | + | \mathrm{f}: \left[ \, 5, \, 6 \, \right] \subset R \longrightarrow R |
</math> | </math> | ||
| - | </ | + | |
| - | + | <br/> | |
| - | + | ||
<math> | <math> | ||
| - | + | x \longrightarrow \mathrm{f} \left( \, x \, \right) \, = \, \frac{1}{x} | |
</math> | </math> | ||
</center> | </center> | ||
| - | + | ||
| + | <br/> | ||
| + | |||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \mathrm{g}: \left[ \, 1, \, 4 \, \right] \subset R \longrightarrow R | |
</math> | </math> | ||
| - | |||
<br/> | <br/> | ||
| - | = | + | <math> |
| + | x \longrightarrow \mathrm{g} \left( \, x \, \right) \, = \, \frac{1}{x} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | son funciones distintas porque sus dominios de definición son diferentes. | ||
<br/> | <br/> | ||
| - | + | Observese que, en ambos casos, la imagen de | |
<math> | <math> | ||
| - | + | x | |
</math> | </math> | ||
| - | + | se calcula de la misma manera ( dividiendo 1 entre | |
| - | + | ||
<math> | <math> | ||
| - | + | x | |
</math> | </math> | ||
| - | + | ). | |
| + | |||
| + | <br/> | ||
| + | |||
| + | Sin embargo, cuando nos dicen que la función es | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \mathrm{f} \left( \, x \, \right) = \frac{1}{x} | |
</math> | </math> | ||
| - | + | </center> | |
| + | y nos piden el dominio, se entiende, que lo que nos están pidiendo es el | ||
| + | mayor dominio posible, el conjunto de todos los números reales | ||
<math> | <math> | ||
| - | + | x | |
</math> | </math> | ||
| - | + | para los cuales existe | |
| - | + | ||
<math> | <math> | ||
| - | \ | + | \frac{1}{x} |
</math> | </math> | ||
| - | + | , es decir, | |
| - | + | ||
<math> | <math> | ||
| - | + | \left\{ | |
| + | \, x \in \mathbb{R} \, \left| \, \exists \mathrm{f} \left( \, x \, \right) | ||
| + | \, \right. | ||
| + | \right\} | ||
</math> | </math> | ||
| - | | + | , que en el ejemplo que estamos considerando es |
<center> | <center> | ||
<math> | <math> | ||
| - | \ | + | \mathbb{R} - \left\{ \, 0 \, \right\} |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
</center> | </center> | ||
| - | + | (Todos los números reales excepto el cero ). | |
| - | + | ||
<br/> | <br/> | ||
| - | == | + | ==Método para hallar el dominio== |
<br/> | <br/> | ||
| - | + | Un procedimiento de obtención del dominio de una función | |
<math> | <math> | ||
| - | \mathrm{f} | + | \mathrm{f} |
</math> | </math> | ||
| - | + | es quitar a | |
<math> | <math> | ||
| - | \ | + | \mathbb{R} |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| - | + | todos los | |
<math> | <math> | ||
| - | + | x | |
</math> | </math> | ||
| - | está | + | en los que la función no está definida. |
<br/> | <br/> | ||
| - | + | En general, la función | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | En la | + | |
<math> | <math> | ||
| - | f | + | \mathrm{f} |
</math> | </math> | ||
| - | + | no está definida en | |
<math> | <math> | ||
| - | + | x | |
</math> | </math> | ||
| - | + | cuando al evaluar | |
| - | + | ||
<math> | <math> | ||
| - | + | \mathrm{f} | |
</math> | </math> | ||
| - | + | en | |
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | nos encontramos con alguno de los siguientes "problemas": | ||
| - | + | # 1. Divisón por cero. | |
| + | |||
| + | # 2. Logaritmo de un número no positivo ( cero o negativo ). | ||
| - | + | # 3. Raíz de orden par de un número negativo. | |
<br/> | <br/> | ||
| - | + | ==Ejemplo== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Veamos como podemos hallar el dominio de | |
| - | + | <center> | |
| - | + | ||
<math> | <math> | ||
| - | + | \mathrm{f} \left( \, x \, \right) = \sqrt{\frac{\log \left( \, x \, \right)}{x - | |
| - | + | 2}} | |
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| - | + | </center> | |
| + | |||
| + | Según lo explicado anteriormente, buscamos primero aquellos valores de | ||
<math> | <math> | ||
| - | + | x | |
</math> | </math> | ||
| - | + | para los cuales no existe | |
<math> | <math> | ||
| - | \mathrm{f} | + | \mathrm{f} \left( \, x \, \right) |
| - | </math> | + | </math>. |
| - | + | ||
| - | + | <br/> | |
| + | |||
| + | La raíz de un número negativo no es un número real, por lo tanto, excluiremos | ||
| + | del dominio aquellos valores de | ||
<math> | <math> | ||
| - | + | x | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| - | + | que sean solución de la inecuación | |
| + | <center> | ||
<math> | <math> | ||
| - | \ | + | 0 > \frac{\log \left( \, x \, \right)}{x - 2} |
</math> | </math> | ||
| - | + | </center> | |
| + | La función | ||
| + | <center> | ||
<math> | <math> | ||
| - | \ | + | \frac{\log \left( \, x \, \right)}{x - 2} |
</math> | </math> | ||
| - | + | </center> | |
| - | + | es negativa cuando | |
| - | < | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | \ | + | \log \left( \, x \, \right) |
</math> | </math> | ||
| - | | + | y |
<math> | <math> | ||
| - | + | x - 2 | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| - | + | tienen diferente signo, es decir, cuando ( caso 1 ) | |
<br/> | <br/> | ||
| - | + | <center> | |
<math> | <math> | ||
| - | \ | + | \left\{ |
| + | \begin{array}{l} | ||
| + | \log \left( \, x \, \right) > 0 | ||
| + | \\ | ||
| + | 0 > x - 2 | ||
| + | \end{array} | ||
| + | \right. | ||
</math> | </math> | ||
| - | + | </center> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | </ | + | |
| - | + | ||
| - | + | o bien, cuando ( caso 2 ) | |
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | |||
<center> | <center> | ||
<math> | <math> | ||
| - | \ | + | \left\{ |
| + | \begin{array}{l} | ||
| + | 0 > \log \left( \, x \, \right) | ||
| + | \\ | ||
| + | x - 2 > 0 | ||
| + | \end{array} | ||
| + | \right. | ||
</math> | </math> | ||
</center> | </center> | ||
| - | + | ||
| - | + | Analicemos primero el caso 1. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | La solución de | |
| - | + | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \ | + | \log \left( \, x \, \right) > 0 |
</math> | </math> | ||
</center> | </center> | ||
| - | + | es | |
<center> | <center> | ||
<math> | <math> | ||
| - | + | x \in \left( \, 1, \, \infty \, \right) | |
</math> | </math> | ||
</center> | </center> | ||
| - | + | mientras que la solución de | |
| + | <center> | ||
<math> | <math> | ||
| - | - | + | 0 > x - 2 |
</math> | </math> | ||
| - | + | </center> | |
| + | es | ||
| + | <center> | ||
<math> | <math> | ||
| - | \infty | + | x \in \left( \, -\infty, \, 2 \, \right) |
| - | </math> | + | </math> |
| - | + | </center> | |
| + | |||
| + | Por lo tanto, el caso 1 se da cuando | ||
| + | <center> | ||
<math> | <math> | ||
| - | \ | + | x \in \left( \, -\infty, \, 2 \, \right) \cap \left( \, 1, \, \infty \, |
| + | \right) = \left( \, 1, \, 2 \, \right) | ||
</math> | </math> | ||
| - | + | </center> | |
<br/> | <br/> | ||
| - | + | Analicemos, a continuación, el caso 2. | |
<br/> | <br/> | ||
| + | La solución de | ||
| + | <center> | ||
| + | <math> | ||
| + | 0 > \log \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | es | ||
| + | <center> | ||
| + | <math> | ||
| + | x \in \left( \, 0, \, 1 \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | mientras que la solución de | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | x - 2 > 0 | |
| + | </math> | ||
| + | </center> | ||
| + | es | ||
| + | <center> | ||
| + | <math> | ||
| + | x \in \left( \, 2, \, \infty \, \right) | ||
</math> | </math> | ||
</center> | </center> | ||
| - | Por lo tanto, | + | Por lo tanto, el caso 2 se da cuando |
| + | <center> | ||
| + | <math> | ||
| + | x \in \left( \, 2, \, \infty \, \right) \cap \left( \, 0, \, 1 \, \right) = | ||
| + | \emptyset | ||
| + | </math> | ||
| + | </center> | ||
| + | Es decir, este caso nunca se da ( | ||
<math> | <math> | ||
| - | \ | + | \emptyset = |
</math> | </math> | ||
| - | + | conjunto vacio ). | |
<br/> | <br/> | ||
| - | + | El dos tampoco está en el dominio de | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | + | \mathrm{f} | |
</math> | </math> | ||
| - | + | porque cuando | |
<math> | <math> | ||
| - | + | x = 2 | |
</math> | </math> | ||
| - | + | se tiene una división por 0 en | |
| + | <center> | ||
<math> | <math> | ||
| - | + | \sqrt{\frac{\log \left( \, x \, \right)}{x - 2}} | |
| - | </math> | + | </math> |
| + | </center> | ||
| + | |||
| + | Concluimos así, que el dominio de | ||
<math> | <math> | ||
| - | + | \mathrm{f} | |
</math> | </math> | ||
| - | + | es | |
| + | <center> | ||
<math> | <math> | ||
| - | + | \mathbb{R} - \left\{ \, 2 \, \right\} - \left( \, 1, \, 2 \, \right) = | |
| - | </math> | + | \left( \, -\infty, \, 1 \, \right] \cup \left( \, 2, \, \infty \, \right) |
| + | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
| - | == | + | ==Dominio y gráfica== |
<br/> | <br/> | ||
| - | El | + | El conocer el dominio de una función |
<math> | <math> | ||
| - | \ | + | \mathrm{f} |
</math> | </math> | ||
| - | + | nos va a permitir identificar bandas o franjas verticales donde la gráfica de la | |
| - | + | función no está ( ningún punto de la gráfica de | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | \ | + | \mathrm{f} |
</math> | </math> | ||
| - | + | se encotraría en dichas franjas o bandas verticales ). | |
| - | + | ||
<br/> | <br/> | ||
| - | == | + | ==Ejemplo== |
<br/> | <br/> | ||
| - | + | En el ejemplo anterior el dominio de | |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | + | es | |
| + | <center> | ||
<math> | <math> | ||
| - | + | \mathbb{R} - \left( \, 1, \, 2 \, \right] | |
</math> | </math> | ||
| - | + | </center> | |
| + | La gráfica de | ||
<math> | <math> | ||
| - | \mathrm{f} | + | \mathrm{f} |
| - | </math> | + | </math> |
| - | + | podría tener algún punto en la recta vertical | |
| - | + | ||
<math> | <math> | ||
| - | \mathrm{ | + | \mathrm{r} |
| - | + | ||
</math> | </math> | ||
| - | | + | de ecuación |
<math> | <math> | ||
| - | + | x = 1 | |
</math> | </math> | ||
| - | + | pero no puede tener ningún punto, ni en la recta vertical | |
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | \mathrm{ | + | \mathrm{s} |
</math> | </math> | ||
| - | + | de ecuación | |
<math> | <math> | ||
| - | + | x = 2 | |
</math> | </math> | ||
| - | | + | ni en ningún punto en la franja vertical delimitadas por las rectas |
<math> | <math> | ||
| - | \mathrm{ | + | \mathrm{r} |
| - | </math> | + | </math> |
| - | + | y | |
| - | + | ||
<math> | <math> | ||
| - | \mathrm{ | + | \mathrm{s} |
| - | + | </math>. | |
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Recorrido y gráfica== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Análogamente, el conocer el dominio de una función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
</math> | </math> | ||
| - | + | nos va a permitir identificar bandas o franjas horizontales donde la gráfica de la | |
| + | función no está ( ningún punto de la gráfica de | ||
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | + | se encotraría en dichas franjas o bandas horizontales ). | |
| - | + | <br/> | |
| - | + | ||
| + | ==Ejemplo== | ||
<br/> | <br/> | ||
| - | + | El recorrido de la función | |
<center> | <center> | ||
<math> | <math> | ||
| - | + | \mathrm{f} \left( \, x \, \right) = \cos \left( \, x \, \right) | |
</math> | </math> | ||
</center> | </center> | ||
| - | + | es | |
<math> | <math> | ||
| - | \left | + | \left[ \, -1, \, 1 \, \right] |
| - | </math> | + | </math>, |
| - | | + | lo cual significa que deberemos dibujar la gráfica en la banda horizontal |
| + | delimitada por las rectas horizontales de ecuaciones | ||
<math> | <math> | ||
| - | + | y = -1 | |
</math> | </math> | ||
| - | + | e | |
<math> | <math> | ||
| - | + | y = 1 | |
| - | </math> | + | </math>, |
| - | + | ya que ningún punto de la gráfica se encuentra fuera de esta banda horizontal. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 10:03 1 ago 2010
Tabla de contenidos |
Definición de dominio
En principio y hablando con rigor, el dominio de una función es parte de la definición de esa función.
Ejemplo
Las funciones
![\mathrm{f}: \left[ \, 5, \, 6 \, \right] \subset R \longrightarrow R
\mathrm{f}: \left[ \, 5, \, 6 \, \right] \subset R \longrightarrow R](/images/math/math-6d69fc070bf4d99f3e1abd1cd6fb30ea.png)
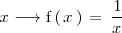
![\mathrm{g}: \left[ \, 1, \, 4 \, \right] \subset R \longrightarrow R
\mathrm{g}: \left[ \, 1, \, 4 \, \right] \subset R \longrightarrow R](/images/math/math-723cadf38fa49eb6be59832152a9192c.png)
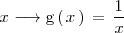
son funciones distintas porque sus dominios de definición son diferentes.
Observese que, en ambos casos, la imagen de
 se calcula de la misma manera ( dividiendo 1 entre
se calcula de la misma manera ( dividiendo 1 entre
 ).
).
Sin embargo, cuando nos dicen que la función es
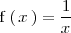
y nos piden el dominio, se entiende, que lo que nos están pidiendo es el
mayor dominio posible, el conjunto de todos los números reales
 para los cuales existe
para los cuales existe
 , es decir,
, es decir,
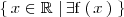 , que en el ejemplo que estamos considerando es
, que en el ejemplo que estamos considerando es
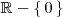
(Todos los números reales excepto el cero ).
Método para hallar el dominio
Un procedimiento de obtención del dominio de una función
 es quitar a
es quitar a
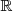 todos los
todos los
 en los que la función no está definida.
en los que la función no está definida.
En general, la función
 no está definida en
no está definida en
 cuando al evaluar
cuando al evaluar
 en
en
 nos encontramos con alguno de los siguientes "problemas":
nos encontramos con alguno de los siguientes "problemas":
- 1. Divisón por cero.
- 2. Logaritmo de un número no positivo ( cero o negativo ).
- 3. Raíz de orden par de un número negativo.
Ejemplo
Veamos como podemos hallar el dominio de
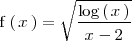
Según lo explicado anteriormente, buscamos primero aquellos valores de
 para los cuales no existe
para los cuales no existe
 .
.
La raíz de un número negativo no es un número real, por lo tanto, excluiremos
del dominio aquellos valores de
 que sean solución de la inecuación
que sean solución de la inecuación
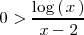
La función
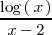
es negativa cuando
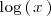 y
y
 tienen diferente signo, es decir, cuando ( caso 1 )
tienen diferente signo, es decir, cuando ( caso 1 )
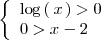
o bien, cuando ( caso 2 )
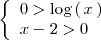
Analicemos primero el caso 1.
La solución de
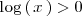
es
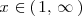
mientras que la solución de
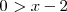
es
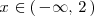
Por lo tanto, el caso 1 se da cuando
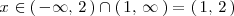
Analicemos, a continuación, el caso 2.
La solución de
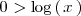
es
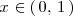
mientras que la solución de
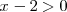
es
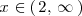
Por lo tanto, el caso 2 se da cuando
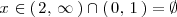
Es decir, este caso nunca se da (
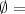 conjunto vacio ).
conjunto vacio ).
El dos tampoco está en el dominio de
 porque cuando
porque cuando
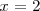 se tiene una división por 0 en
se tiene una división por 0 en
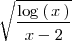
Concluimos así, que el dominio de
 es
es
![\mathbb{R} - \left\{ \, 2 \, \right\} - \left( \, 1, \, 2 \, \right) =
\left( \, -\infty, \, 1 \, \right] \cup \left( \, 2, \, \infty \, \right)
\mathbb{R} - \left\{ \, 2 \, \right\} - \left( \, 1, \, 2 \, \right) =
\left( \, -\infty, \, 1 \, \right] \cup \left( \, 2, \, \infty \, \right)](/images/math/math-442584f51243704cdc59eaaac3d4aad2.png)
Dominio y gráfica
El conocer el dominio de una función
 nos va a permitir identificar bandas o franjas verticales donde la gráfica de la
función no está ( ningún punto de la gráfica de
nos va a permitir identificar bandas o franjas verticales donde la gráfica de la
función no está ( ningún punto de la gráfica de
 se encotraría en dichas franjas o bandas verticales ).
se encotraría en dichas franjas o bandas verticales ).
Ejemplo
En el ejemplo anterior el dominio de
 es
es
![\mathbb{R} - \left( \, 1, \, 2 \, \right]
\mathbb{R} - \left( \, 1, \, 2 \, \right]](/images/math/math-e1f05b0b4185fbb63a0e0ff24c7efbd5.png)
La gráfica de
 podría tener algún punto en la recta vertical
podría tener algún punto en la recta vertical
 de ecuación
de ecuación
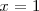 pero no puede tener ningún punto, ni en la recta vertical
pero no puede tener ningún punto, ni en la recta vertical
 de ecuación
de ecuación
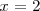 ni en ningún punto en la franja vertical delimitadas por las rectas
ni en ningún punto en la franja vertical delimitadas por las rectas
 y
y
 .
.
Recorrido y gráfica
Análogamente, el conocer el dominio de una función
 nos va a permitir identificar bandas o franjas horizontales donde la gráfica de la
función no está ( ningún punto de la gráfica de
nos va a permitir identificar bandas o franjas horizontales donde la gráfica de la
función no está ( ningún punto de la gráfica de
 se encotraría en dichas franjas o bandas horizontales ).
se encotraría en dichas franjas o bandas horizontales ).
Ejemplo
El recorrido de la función
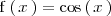
es
![\left[ \, -1, \, 1 \, \right]
\left[ \, -1, \, 1 \, \right]](/images/math/math-835b91871a82c41933594d58cb622152.png) ,
lo cual significa que deberemos dibujar la gráfica en la banda horizontal
delimitada por las rectas horizontales de ecuaciones
,
lo cual significa que deberemos dibujar la gráfica en la banda horizontal
delimitada por las rectas horizontales de ecuaciones
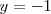 e
e
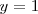 ,
ya que ningún punto de la gráfica se encuentra fuera de esta banda horizontal.
,
ya que ningún punto de la gráfica se encuentra fuera de esta banda horizontal.



