Navegación
Funciones y gráficas
De Wikillerato
m (Revertidas las ediciones realizadas por 89.7.158.180 (Talk); a la última edición de Laura.2mdc) |
|||
| Línea 11: | Línea 11: | ||
x | x | ||
</math> | </math> | ||
| - | de un subconjunto no | + | de un subconjunto no vacio |
<math> | <math> | ||
D | D | ||
| Línea 69: | Línea 69: | ||
<br/> | <br/> | ||
| - | Una función se define ''''' | + | Una función se define '''''explicitamente''''' si viene dada como |
<math> | <math> | ||
y \, = \, \mathrm{f} \left( \, x \, \right) | y \, = \, \mathrm{f} \left( \, x \, \right) | ||
| Línea 77: | Línea 77: | ||
y | y | ||
</math> | </math> | ||
| - | , | + | , está despejada. |
<br/> | <br/> | ||
| Línea 89: | Línea 89: | ||
\, = \, 0 | \, = \, 0 | ||
</math> | </math> | ||
| - | , esto es, si la función se | + | , esto es, si la función se define mediante una expresión algebraica igualada a cero. |
<br/> | <br/> | ||
| Línea 162: | Línea 162: | ||
<br/> | <br/> | ||
| + | |||
| + | ==Características de una función== | ||
| + | |||
| + | Las características mas importantes de una función son: | ||
| + | |||
| + | # [[Dominio y recorrido|Dominio y recorrido.]] | ||
| + | |||
| + | # [[Periodicidad|Existencia o no de periodicidad.]] | ||
| + | |||
| + | # [[Simetrías|Existencia o no de simetrías.]] | ||
| + | |||
| + | # [[Funciones acotadas|Acotada o no acotada ( superior y/o inferiormente ).]] | ||
| + | |||
| + | # [[Extremos relativos|Existencia o no de extremos relativos.]] | ||
| + | |||
| + | # [[Funciones acotadas|Existencia o no de extremos absolutos.]] | ||
| + | |||
| + | # [[Continuidad|Puntos de discontinuidad.]] | ||
| + | |||
| + | # [[Puntos de corte con los ejes de coordenadas|Puntos de corte con los ejes de coordenadas.]] | ||
| + | |||
| + | # [[Signo de la función|Signo de la función ( para que valores de la variable independiente la función | ||
| + | es positiva y para que valores es negativa ).]] | ||
| + | |||
| + | # [[Crecimiento y decrecimiento|Donde la función es creciente y donde decreciente.]] | ||
| + | |||
| + | # [[Cancavidad y convexidad|Concavidad y convexidad.]] | ||
| + | |||
| + | # [[Asintotas|Asíntotas ( horizontales, verticales y oblicuas ).]] | ||
| + | |||
| + | La representación gráfica de una función se lleva a cabao para | ||
| + | visualizar de golpe las características mas importantes de dicha función, por eso, antes de dibujar la gráfica de la función es | ||
| + | importante determinar analiticamente cuales son esas características. | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 09:16 3 ago 2010
Tabla de contenidos |
Definición
Una función real de variable real es toda correspondencia
que asocia a cada elemento
de un subconjunto no vacio
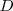de
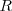un único número real. La expresamos como:
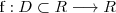
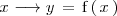
es la variable independiente e
la variable dependiente.
Al conjunto,
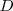, de valores que toma la variable independiente
se le llama dominio de la función.
Al conjunto de valores que toma la variable dependiente
se le llama recorrido de la función.
Una función se define explicitamente si viene dada como
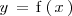, es decir, si la variable dependiente,
, está despejada.
Una función se define implícitamente si viene dada en la forma
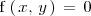, esto es, si la función se define mediante una expresión algebraica igualada a cero.
Ejemplo
La función
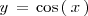está expresada en forma explícita.
La función
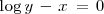está expresada en forma implícita.
Gráfica
La gráfica de una función
es el conjunto de puntos del plano definido de la siguiente forma:
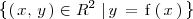
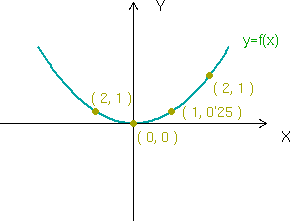
Ejemplo
La figura de abajo muestra la gráfica de la funcion
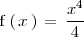y cuatro puntos de la misma:
Características de una función
Las características mas importantes de una función son:
La representación gráfica de una función se lleva a cabao para visualizar de golpe las características mas importantes de dicha función, por eso, antes de dibujar la gráfica de la función es importante determinar analiticamente cuales son esas características.
Tweet
