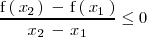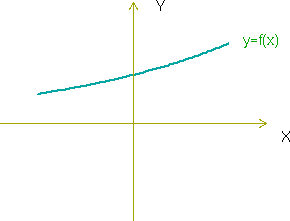Navegación
Funciones crecientes y decrecientes
De Wikillerato
m (Revertidas las ediciones realizadas por 189.139.39.158 (Talk); a la última edición de Laura.2mdc) |
(→Función creciente en un intervalo) |
||
| Línea 135: | Línea 135: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \frac{\ | + | \frac{\fdffdfdfdbfbgfhtyutyjmathrm{f}\left( \, x_2 \, \right) \, - \, \mathrm{f}\left( \, x_1 \, \right)}{x_2 |
\, - \, x_1} \ge 0 | \, - \, x_1} \ge 0 | ||
</math> | </math> | ||
Revisión de 01:29 4 oct 2009
Tabla de contenidos |
Función estrictamente creciente en un intervalo
Una función
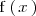es estrictamente creciente en un intervalo
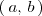, si para dos valores cualesquiera del intervalo,
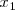y
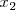, se cumple que:
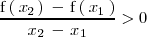
Cuando en la gráfica de una función estrictamente creciente nos movemos hacia la derecha tambien nos movemos hacia arriba:
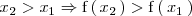
Una función
es estrictamente creciente en el punto de abcisa
si existe algun número positivo
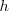tal que
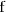es estrictamente creciente en el intervalo
.
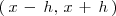De esta esta definición se deduce que si
es derivable en
y
es estrictamente creciente en el punto de abcisa
, entonces
.
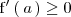Función creciente en un intervalo
Una función
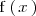es creciente en un intervalo
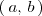, si para dos valores cualesquiera del intervalo,
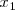y
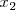, se cumple que:
[Unparseable or potentially dangerous latex formula. Error 3 ]
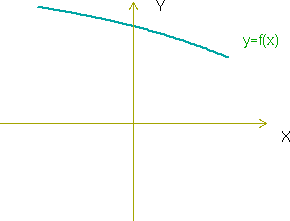
Función estrictamente decreciente en un intervalo
Una función
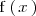es estrictamente decreciente en un intervalo
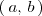, si para dos valores cualesquiera del intervalo,
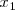y
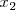, se cumple que:
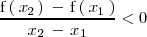
Cuando en la gráfica de una función estrictamente decreciente nos movemos hacia la derecha tambien nos movemos hacia abajo:
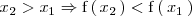
Una función
es estrictamente decreciente en el punto de abcisa
si existe algun número positivo
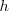tal que
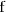es estrictamente decreciente en el intervalo
.
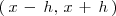De esta esta definición se deduce que si
es derivable en
y
es estrictamente decreciente en el punto de abcisa
, entonces
.
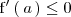Función decreciente en un intervalo
Una función
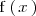es decreciente en un intervalo
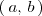, si para dos valores cualesquiera del intervalo,
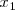y
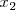, se cumple que:
