Navegación
Sistemas axonométricos ortogonales y oblicuos
De Wikillerato
(→Fundamento del sistema) |
m (Revertidas las ediciones realizadas por 83.59.182.22 (Talk); a la última edición de Laura.2mdc) |
||
| Línea 4: | Línea 4: | ||
Los sistemas axonométricos están basados en la proyección cilíndrica de los objetos sobre tres planos de proyección que forman un triedro trirrectángulo y la proyección del objeto y sus tres proyecciones sobre un plano llamado plano del cuadro. Por lo tanto cada objeto tiene cuatro proyecciones, la directa y las proyecciones sobre el plano horizontal y los dos verticales. Además esto implica la aparición de coeficientes de reducción que son razón entre la magnitud del segmento proyectado en cada plano y la del segmento real. | Los sistemas axonométricos están basados en la proyección cilíndrica de los objetos sobre tres planos de proyección que forman un triedro trirrectángulo y la proyección del objeto y sus tres proyecciones sobre un plano llamado plano del cuadro. Por lo tanto cada objeto tiene cuatro proyecciones, la directa y las proyecciones sobre el plano horizontal y los dos verticales. Además esto implica la aparición de coeficientes de reducción que son razón entre la magnitud del segmento proyectado en cada plano y la del segmento real. | ||
| - | |||
| - | |||
Los sistemas '''axonométricos ortogonales''' se basan en la proyección cilíndrica ortogonal. Son las axonometrías isométrica, dimétricas y trimétricas. | Los sistemas '''axonométricos ortogonales''' se basan en la proyección cilíndrica ortogonal. Son las axonometrías isométrica, dimétricas y trimétricas. | ||
| Línea 22: | Línea 20: | ||
Son los métodos geométricos que aplicaremos a las características de los sistemas axonométricos. | Son los métodos geométricos que aplicaremos a las características de los sistemas axonométricos. | ||
| - | |||
===Resolución de problemas=== | ===Resolución de problemas=== | ||
Se trata de resolver problemas básicos de representación, intersecciones con rectas y planos y verdaderas magnitudes. | Se trata de resolver problemas básicos de representación, intersecciones con rectas y planos y verdaderas magnitudes. | ||
| - | + | ||
[[Categoría:Dibujo]] | [[Categoría:Dibujo]] | ||
Revisión de 08:29 10 may 2010
Uno o más usuarios están trabajando actualmente en extender este artículo.
Es posible que, a causa de ello, haya lagunas de contenido o deficiencias de formato. Por favor, antes de realizar correcciones mayores o reescrituras, contacta con ellos en la página de discusión.
Fundamento del sistema
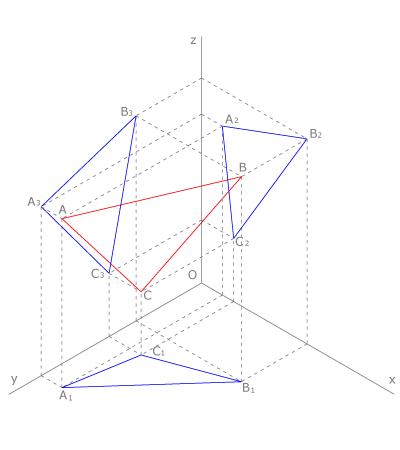
Los sistemas axonométricos están basados en la proyección cilíndrica de los objetos sobre tres planos de proyección que forman un triedro trirrectángulo y la proyección del objeto y sus tres proyecciones sobre un plano llamado plano del cuadro. Por lo tanto cada objeto tiene cuatro proyecciones, la directa y las proyecciones sobre el plano horizontal y los dos verticales. Además esto implica la aparición de coeficientes de reducción que son razón entre la magnitud del segmento proyectado en cada plano y la del segmento real.
Los sistemas axonométricos ortogonales se basan en la proyección cilíndrica ortogonal. Son las axonometrías isométrica, dimétricas y trimétricas.
En la figura vemos la representación isométrica de un triángulo 
que se proyecta sobre el primer plano vertical como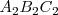 
, sobre el segundo plano vertical como 
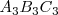y sobre el plano horizontal como 
.
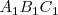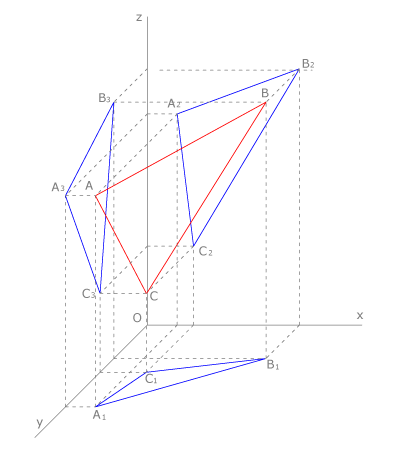
Los sistemas axonométricos oblicuos se basan en la proyección cilíndrica oblicua o paralela, como las perspectivas caballera y militar.
En la figura vemos la representación caballera de un triángulo que se proyecta sobre el primer plano vertical como 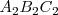, sobre el segundo plano vertical como 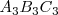y sobre el plano horizontal como .
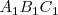Métodos operativos
Son los métodos geométricos que aplicaremos a las características de los sistemas axonométricos.
Resolución de problemas
Se trata de resolver problemas básicos de representación, intersecciones con rectas y planos y verdaderas magnitudes.
Tweet
