Procedimiento para factorizar un polinomio
De Wikillerato
| Línea 5: | Línea 5: | ||
<br/> | <br/> | ||
| - | 1. Sacamos <math> x </math> factor | + | 1. Sacamos <math> x </math> factor común, si ello es posible. |
<br/> | <br/> | ||
| Línea 19: | Línea 19: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | resolvemos la | + | resolvemos la ecuación |
<center> | <center> | ||
<math> | <math> | ||
| Línea 26: | Línea 26: | ||
</center> | </center> | ||
| - | Si esta | + | Si esta ecuación no tiene solución, el polinomio |
<math> | <math> | ||
\mathrm{P} \left( \, x \, \right) | \mathrm{P} \left( \, x \, \right) | ||
</math> | </math> | ||
| - | es irreducible | + | es irreducible, |
| - | + | pero si la ecuación anterior tiene soluciones | |
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
r_1 | r_1 | ||
| Línea 54: | Línea 51: | ||
</center> | </center> | ||
| - | + | Puede ocurrir que | |
| + | <math> | ||
| + | r_1 | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | r_2 | ||
| + | </math> | ||
| + | coincidan ( sean iguales ). | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si el polinomio | ||
| + | <center> | ||
<math> | <math> | ||
\mathrm{P} \left( \, x \, \right) = a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + | \mathrm{P} \left( \, x \, \right) = a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + | ||
\ldots + a_1 \cdot x + a_0 | \ldots + a_1 \cdot x + a_0 | ||
</math> | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
| - | + | <span | |
| - | + | style = 'color:#00aa00'> | |
| - | + | • | |
| + | </span> es de grado mayor que dos | ||
<br/> | <br/> | ||
| - | utilizamos regla de | + | <span |
| + | style = 'color:#00aa00'> | ||
| + | • | ||
| + | </span> sus coeficientes son enteros, y | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <span | ||
| + | style = 'color:#00aa00'> | ||
| + | • | ||
| + | </span> <math> \frac{a_0}{a_n} </math> es un número entero | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | utilizamos [[Regla de Ruffini|regla de Ruffini]] con los divisores de <math> | ||
\frac{a_0}{a_n} </math> y el polinomio | \frac{a_0}{a_n} </math> y el polinomio | ||
<math> | <math> | ||
| Línea 76: | Línea 102: | ||
<br/> | <br/> | ||
| - | | + | <math> \mathrm{P} \left( \, a \, \right) = 0 </math> si y solo si <math> x - a </math> es divisor de <math> \mathrm{P} \left( \, x \, \right) </math>. |
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Ejemplo== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Factorizemos el polinomio: | ||
| + | <center> | ||
<math> | <math> | ||
| - | \mathrm{P} \left( \, | + | \mathrm{P} \left( \, x \, \right) = 2x^4 - 12x^3 + 22x^2 - 12x |
</math> | </math> | ||
| - | + | </center> | |
| + | Como se puede sacar un | ||
<math> | <math> | ||
| - | x | + | x |
</math> | </math> | ||
| - | es | + | factor común, eso es lo primero que hacemos: |
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{P} \left( \, x \, \right) = 2x^4 - 12x^3 + 22x^2 - 12x = | ||
| + | x \cdot \left( \, 2x^3 - 12x^2 + 22x - 12 \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | A continuación factorizamos | ||
| + | <center> | ||
| + | <math> | ||
| + | 2x^3 - 12x^2 + 22x - 12 | ||
| + | </math> | ||
| + | </center> | ||
| + | Como se trata de un polinomio de grado mayor que dos, utilizamos Ruffini para ver | ||
| + | si podemos encontrar alguna de sus raices. Los candidatos a raiz que | ||
| + | consideramos son los divisores de | ||
| + | <math> | ||
| + | \frac{-12}{2} = -6 | ||
| + | </math>, | ||
| + | que son | ||
| + | <math> | ||
| + | -1, 1, -2, 2, -3, 3, -6, 6 | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | De este modo, se puede obtener que 3 es una raiz de | ||
<math> | <math> | ||
\mathrm{P} \left( \, x \, \right) | \mathrm{P} \left( \, x \, \right) | ||
| - | </math> | + | </math>, |
| + | es decir, | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{P} \left( \, 3 \, \right) = 0 | ||
| + | </math> | ||
| + | </center> | ||
| + | y que | ||
| + | <center> | ||
| + | <math> | ||
| + | 2x^3 - 12x^2 + 22x - 12 = \left( \, x - 3 \, \right) \cdot | ||
| + | \left( | ||
| + | \, 2x^2 - 6x + 4 \, | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | Finalmente, factorizamos el polinomio | ||
| + | <center> | ||
| + | <math> | ||
| + | x^2 - 3x + 2 | ||
| + | </math> | ||
| + | </center> | ||
| + | resolviendo la ecuación | ||
| + | <center> | ||
| + | <math> | ||
| + | 2x^2 - 6x + 4 | ||
| + | </math> | ||
| + | </center> | ||
| + | cuyas soluciones son 2 y 1, de manera que | ||
| + | <center> | ||
| + | <math> | ||
| + | 2x^2 - 6x + 4 = 2 \left( \, x - 1 \, \right) \cdot \left( \, x - 2 \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | y, por tanto | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{P} \left( \, x \, \right) = 2 \left( \, x - 1 \, \right) \cdot \left( \, | ||
| + | x - 2 \, \right) \cdot \left( \, x - 3 \, \right) | ||
| + | </math> | ||
| + | </center> | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 10:54 19 sep 2010
Procedimiento para factorizar un polinomio
1. Sacamos  factor común, si ello es posible.
factor común, si ello es posible.
2. Si el polinomio
 es de grado dos:
es de grado dos:
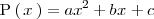
resolvemos la ecuación
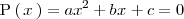
Si esta ecuación no tiene solución, el polinomio
 es irreducible,
pero si la ecuación anterior tiene soluciones
es irreducible,
pero si la ecuación anterior tiene soluciones
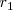 y
y
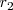 ,
entonces podemos factorizar
,
entonces podemos factorizar
 de la siguiente manera:
de la siguiente manera:
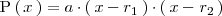
Puede ocurrir que
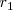 y
y
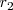 coincidan ( sean iguales ).
coincidan ( sean iguales ).
Si el polinomio
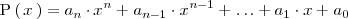
• es de grado mayor que dos
• sus coeficientes son enteros, y
•
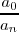 es un número entero
es un número entero
utilizamos regla de Ruffini con los divisores de [Unparseable or potentially dangerous latex formula. Error 3 ] y el polinomio
 .
.
si y solo si
es divisor de [Unparseable or potentially dangerous latex formula. Error 3 ].
Ejemplo
Factorizemos el polinomio:
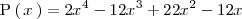
Como se puede sacar un
 factor común, eso es lo primero que hacemos:
factor común, eso es lo primero que hacemos:
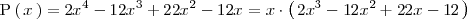
A continuación factorizamos
[Unparseable or potentially dangerous latex formula. Error 3 ]
Como se trata de un polinomio de grado mayor que dos, utilizamos Ruffini para ver
si podemos encontrar alguna de sus raices. Los candidatos a raiz que
consideramos son los divisores de
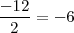 ,
que son
[Unparseable or potentially dangerous latex formula. Error 3 ]
,
que son
[Unparseable or potentially dangerous latex formula. Error 3 ]
De este modo, se puede obtener que 3 es una raiz de
 ,
es decir,
,
es decir,
[Unparseable or potentially dangerous latex formula. Error 3 ]
y que
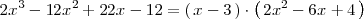
Finalmente, factorizamos el polinomio
[Unparseable or potentially dangerous latex formula. Error 3 ]
resolviendo la ecuación
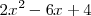
cuyas soluciones son 2 y 1, de manera que
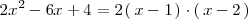
y, por tanto
[Unparseable or potentially dangerous latex formula. Error 3 ]



