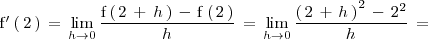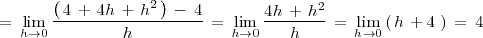Definición de derivada
De Wikillerato
(Diferencias entre revisiones)
| Línea 6: | Línea 6: | ||
<math> | <math> | ||
x \, = \, a | x \, = \, a | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
</math> | </math> | ||
, si existe, es el valor del limite: | , si existe, es el valor del limite: | ||
| Línea 27: | Línea 20: | ||
<br/> | <br/> | ||
| - | Si | + | Si este limite es un número real, la función |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
| Línea 54: | Línea 40: | ||
</math> | </math> | ||
no es derivable en dicho punto. | no es derivable en dicho punto. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La derivada de la función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | en | ||
| + | <math> | ||
| + | x = a | ||
| + | </math> | ||
| + | se denota por | ||
| + | <math> | ||
| + | \mathrm{f}^\prime | ||
| + | \left( | ||
| + | \, a \, | ||
| + | \right) | ||
| + | </math> | ||
<br/> | <br/> | ||
| Línea 101: | Línea 105: | ||
<br/> | <br/> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 10:16 2 ene 2011
La derivada de la función
 en el punto
en el punto
 , si existe, es el valor del limite:
, si existe, es el valor del limite:
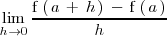 .
.
Si este limite es un número real, la función
 es derivable en
es derivable en
 .
Si
.
Si
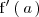 no es un número real o el límite no existe, la función
no es un número real o el límite no existe, la función
 no es derivable en dicho punto.
no es derivable en dicho punto.
La derivada de la función
 en
en
 se denota por
se denota por
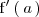
Ejemplo
Calculemos la derivada de
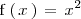 en
en
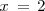 :
: