La derivada como una tasa de variación instantánea
De Wikillerato
| Línea 19: | Línea 19: | ||
y | y | ||
</math> | </math> | ||
| - | , se puede ver como una función, | + | , se puede ver como una función, |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
| Línea 60: | Línea 60: | ||
<br/> | <br/> | ||
| - | En general, la tasa de variación media de la función | + | En general, la tasa de variación media de la función |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | + | en el periodo que va desde el instante | |
<math> | <math> | ||
t_1 | t_1 | ||
| Línea 89: | Línea 89: | ||
<br/> | <br/> | ||
| - | La '''''tasa de variación instantánea''''' de la función | + | La '''''tasa de variación instantánea''''' de la función |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | + | en el instante | |
<math> | <math> | ||
x \, = \, t_1 | x \, = \, t_1 | ||
| Línea 105: | Línea 105: | ||
t_1 | t_1 | ||
</math> | </math> | ||
| - | en la '''''tasa de variación media''''' de la función | + | en la '''''tasa de variación media''''' de la función |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | + | en el periodo | |
<math> | <math> | ||
\left[ | \left[ | ||
\, t_1, \, t_2 \, | \, t_1, \, t_2 \, | ||
\right]. | \right]. | ||
| - | </math> | + | </math>. Por tanto, la '''''tasa de variación instantánea''''' de la función |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | + | en el instante | |
<math> | <math> | ||
x \, = \, t_1 | x \, = \, t_1 | ||
| Línea 134: | Línea 134: | ||
<br/> | <br/> | ||
| - | que es precisamente la [[Definición de derivada|derivada]] de la función | + | que es precisamente la [[Definición de derivada|derivada]] de la función |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | + | en el instante | |
<math> | <math> | ||
x \, = \, t_1 | x \, = \, t_1 | ||
Revisión de 10:38 2 ene 2011
Tasa de variación media
Supongamos que un coche de fórmula uno se mueve en una carretera totalmente recta. A distintas distancias de la salida se registran los tiempos de paso, obteniendose la siguiente tabla:
En este caso, la posición,
 , se puede ver como una función,
, se puede ver como una función,
 , del tiempo,
, del tiempo,
 ; es decir:
; es decir:
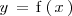
La tasa de variación media de la posición en el intervalo de tiempo desde el
instante
 al instante
al instante
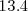 es:
es:
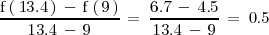
En general, la tasa de variación media de la función
 en el periodo que va desde el instante
en el periodo que va desde el instante
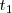 hasta el instante
hasta el instante
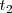 se define como el cociente:
se define como el cociente:
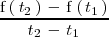
Tasa de variación instantánea
La tasa de variación instantánea de la función
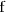 en el instante
en el instante
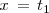 se obtiene haciendo tender
se obtiene haciendo tender
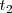 a
a
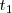 en la tasa de variación media de la función
en la tasa de variación media de la función
 en el periodo
en el periodo
![\left[
</p>
<pre> \, t_1, \, t_2 \,
</pre>
<p>\right].
\left[
</p>
<pre> \, t_1, \, t_2 \,
</pre>
<p>\right].](/images/math/math-f6a1e252d4568b949fe4c330b015c3c3.png) . Por tanto, la tasa de variación instantánea de la función
. Por tanto, la tasa de variación instantánea de la función
 en el instante
en el instante
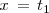 es
es
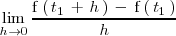
que es precisamente la derivada de la función
 en el instante
en el instante
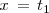 .
.
NOTA: En el límite anterior
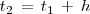 .
.




