Extremos relativos
De Wikillerato
m (Revertidas las ediciones realizadas por 83.50.23.160 (Talk); a la última edición de 213.97.196.225) |
(→Ejercicios Resueltos) |
||
| Línea 190: | Línea 190: | ||
==Ejercicios Resueltos== | ==Ejercicios Resueltos== | ||
| - | + | {{problemas}}* [http://www.selectividad.tv/S_M_2_1_20_S_asintotas_extremos_relativos_y_grafica_de_una_funcion.html Asíntotas, extremos relativos y gráfica de una función] | |
| + | * [http://www.selectividad.tv/S_M_2_1_6_S_extremos_de_una_funcion_polinomica.html Extremos de una función polinómica] | ||
| - | |||
| - | |||
| - | |||
| - | |||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión actual
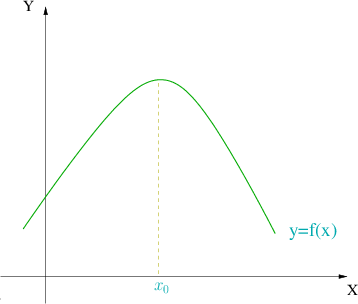
Máximo relativo
Una función
 alcanza un máximo relativo en el punto de abcisa
alcanza un máximo relativo en el punto de abcisa
 si existe un numero positivo
si existe un numero positivo
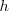 de forma que
de forma que
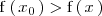 para todos los puntos
para todos los puntos
 del intervalo
del intervalo
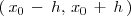 .
.
Si
 es derivable en
es derivable en
 y
y
 alcanza un máximo relativo en el punto de abcisa
alcanza un máximo relativo en el punto de abcisa
 entonces
entonces
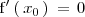 .
.
Si la función
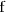 es continua, el que
es continua, el que
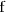 tenga un máximo relativo en un punto significa que la función es creciente a la
izquierda y decreciente a la derecha de ese punto.
tenga un máximo relativo en un punto significa que la función es creciente a la
izquierda y decreciente a la derecha de ese punto.
Si
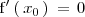 y
y
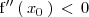 entonces
entonces
 tiene una máximo relativo en el punto de abcisa
tiene una máximo relativo en el punto de abcisa
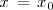 .
.
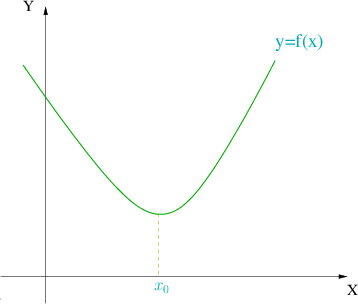
Mínimo relativo
Una función
 alcanza un mínimo relativo en el punto de abcisa
alcanza un mínimo relativo en el punto de abcisa
 si existe un numero positivo
si existe un numero positivo
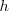 de forma que
de forma que
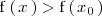 para todos los puntos
para todos los puntos
 del intervalo
del intervalo
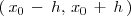 .
.
Si
 es derivable en
es derivable en
 y
y
 alcanza un mínimo relativo en el punto de abcisa
alcanza un mínimo relativo en el punto de abcisa
 entonces
entonces
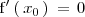 .
.
Si la función
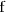 es continua, el que
es continua, el que
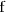 tenga un mínimo relativo en un punto significa que la función es decreciente a la
izquierda y creciente a la derecha de ese punto.
tenga un mínimo relativo en un punto significa que la función es decreciente a la
izquierda y creciente a la derecha de ese punto.
Si
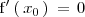 y
y
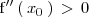 entonces
entonces
 tiene una mínimo relativo en el punto de abcisa
tiene una mínimo relativo en el punto de abcisa
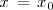 .
.
Ejercicios Resueltos
También te pueden interesar los siguientes ejercicios resueltos de selectividad