Navegación
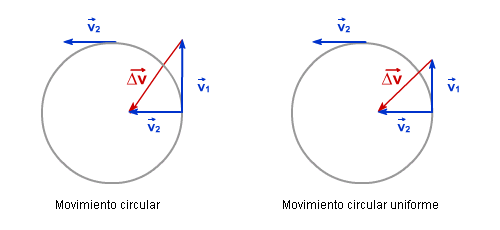
Movimiento circular uniforme
De Wikillerato
| Línea 5: | Línea 5: | ||
[[Imagen:movimiento_circular.gif]] | [[Imagen:movimiento_circular.gif]] | ||
| - | Esta aceleración puede estudiarse referida a un sistema cartesiano con ejes fijos, tal y como estudiado hasta ahora, de modo que <math> \vec a = a_x\vec i + a_y\vec j</math> | + | Esta aceleración puede estudiarse referida a un sistema cartesiano con ejes fijos, tal y como estudiado hasta ahora, de modo que <math> \vec a = a_x\vec i + a_y\vec j</math>. |
| - | Sin embargo, podremos abordar también el estudio de las componentes de la aceleración referidas a un sistema de ejes ortogonales con origen en el punto que ocupa el móvil, en cada instante, en el curso de su movimiento, y de modo que la dirección de uno de esos ejes coincida siempre con la dirección de la tangente a la trayectoria, es decir, con la dirección de la velocidad. El otro eje, necesariamente perpendicular al anterior, tendrá pues la dirección de la perpendicular a la tangente en cada punto, es decir, la dirección del radio del círculo, y que denominaremos dirección normal. A las componentes de la aceleración de este modo obtenidas, se llamarán componentes intrínsecas de la aceleración. Llamaremos <math>\tau</math> al vector unitario en la dirección de la tangente y <math>\eta</math> al vector unitario en la dirección de la normal. Estos dos vectores, aunque de módulo igual a 1, serán variables puesto que su dirección varía constantemente en el curso del tiempo. | + | Sin embargo, podremos abordar también el estudio de las componentes de la aceleración referidas a un sistema de ejes ortogonales con origen en el punto que ocupa el móvil, en cada instante, en el curso de su movimiento, y de modo que la dirección de uno de esos ejes coincida siempre con la dirección de la tangente a la trayectoria, es decir, con la dirección de la velocidad. El otro eje, necesariamente perpendicular al anterior, tendrá pues la dirección de la perpendicular a la tangente en cada punto, es decir, la dirección del radio del círculo, y que denominaremos dirección normal. A las componentes de la aceleración de este modo obtenidas, se llamarán componentes intrínsecas de la aceleración. Llamaremos <math>\vec\tau</math> al vector unitario en la dirección de la tangente y <math>\vec\eta</math> al vector unitario en la dirección de la normal. Estos dos vectores, aunque de módulo igual a 1, serán variables puesto que su dirección varía constantemente en el curso del tiempo. |
Revisión de 12:41 5 dic 2006
Hemos estudiado la variación del vector velocidad, es decir, la aceleración, en un sistema de coordenadas ortogonal, de dos o de tres dimensiones y el caso particular de un movimiento rectilíneo.
Pero veamos que ocurre en el caso de que el movimiento sea circular. Como en cualquier caso, el vector velocidad es siempre tangente a la trayectoria, y dado que es un vector, aún cuando su módulo permaneciese constante, su dirección variará en todo instante, y teniendo en cuenta la definición que hemos aceptado para la aceleración, al variar la dirección de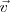 
habrá una variación de 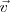y, en consecuencia, existirá una aceleración.
Esta aceleración puede estudiarse referida a un sistema cartesiano con ejes fijos, tal y como estudiado hasta ahora, de modo que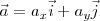 
.
Sin embargo, podremos abordar también el estudio de las componentes de la aceleración referidas a un sistema de ejes ortogonales con origen en el punto que ocupa el móvil, en cada instante, en el curso de su movimiento, y de modo que la dirección de uno de esos ejes coincida siempre con la dirección de la tangente a la trayectoria, es decir, con la dirección de la velocidad. El otro eje, necesariamente perpendicular al anterior, tendrá pues la dirección de la perpendicular a la tangente en cada punto, es decir, la dirección del radio del círculo, y que denominaremos dirección normal. A las componentes de la aceleración de este modo obtenidas, se llamarán componentes intrínsecas de la aceleración. Llamaremos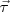 
al vector unitario en la dirección de la tangente y 
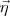al vector unitario en la dirección de la normal. Estos dos vectores, aunque de módulo igual a 1, serán variables puesto que su dirección varía constantemente en el curso del tiempo.
