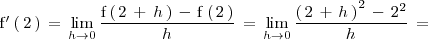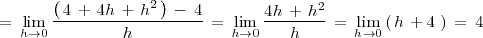Definición de derivada
De Wikillerato
(Diferencias entre revisiones)
| Línea 7: | Línea 7: | ||
x \, = \, a | x \, = \, a | ||
</math> | </math> | ||
| - | , | + | , |
<math> | <math> | ||
\mathrm{f}^\prime | \mathrm{f}^\prime | ||
\left( | \left( | ||
| - | + | \, a \, | |
\right) | \right) | ||
| - | + | </math> | |
| + | , si existe, es el valor del limite: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{h \to 0} \frac{\mathrm{f}\left( \, a \, + \, h \, \right) \, - \, | ||
\mathrm{f} \left( \, a \, \right)}{h} | \mathrm{f} \left( \, a \, \right)}{h} | ||
</math>. | </math>. | ||
| + | </center> | ||
<br/> | <br/> | ||
Revisión de 16:11 11 ene 2007
La derivada de la función
 en el punto
en el punto
 ,
,
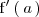 , si existe, es el valor del limite:
, si existe, es el valor del limite:
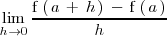 .
.
Si
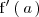 es un número real, la función
es un número real, la función
 es derivable en
es derivable en
 .
Si
.
Si
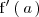 no es un número real o el límite no existe, la función
no es un número real o el límite no existe, la función
 no es derivable en dicho punto.
no es derivable en dicho punto.
Ejemplo
Calculemos la derivada de
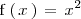 en
en
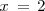 :
: