Significado geométrico de la derivada
De Wikillerato
| Línea 118: | Línea 118: | ||
<math> | <math> | ||
\infty | \infty | ||
| - | </math>. | + | </math>. Como la pendiente de |
<math> | <math> | ||
s_n | s_n | ||
</math> | </math> | ||
| - | es una [[ | + | es una [[La derivada como una tasa de variación instantánea|tasa de variación |
| - | + | media]]: | |
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
<math> | <math> | ||
| - | + | \frac{\mathrm{f} \left( \, A_{n,x} \, \right) \, - \, \mathrm{f} \left( \, A_x \, | |
| + | \right)}{A_{n,x} \, - \, A_x} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | su limite cuando | ||
| + | <math> | ||
| + | n \to \infty | ||
</math> | </math> | ||
es una [[La derivada como una tasa de variación instantánea|tasa de variación instantánea]], la [[Definición de derivada|derivada]] de | es una [[La derivada como una tasa de variación instantánea|tasa de variación instantánea]], la [[Definición de derivada|derivada]] de | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | en | ||
| + | <math> | ||
| + | A_x | ||
| + | </math>. Es decir la pendiente de | ||
| + | <math> | ||
| + | t | ||
| + | </math> | ||
| + | es la derivada de | ||
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
Revisión de 18:36 11 ene 2007
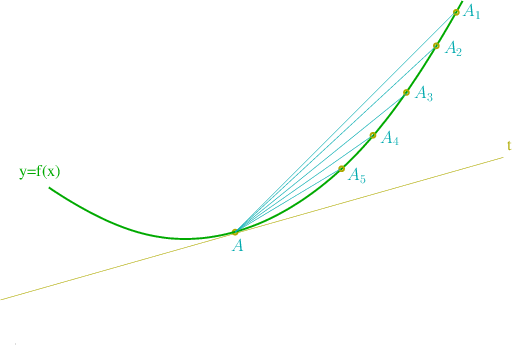
Consideremos la grafica de una función
 . Tomemos un punto
. Tomemos un punto
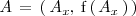 en dicha grafica y consideremos una sucesión de puntos
en dicha grafica y consideremos una sucesión de puntos
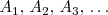 en la grafica de
en la grafica de
 . Supongamos que todos estos puntos estan a la derecha de
. Supongamos que todos estos puntos estan a la derecha de
 y que cuando
y que cuando
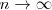 ,
,
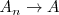 .
.
La recta que pasa por los puntos
 y
y
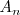 es una secante a la grafica de la función
es una secante a la grafica de la función
 . De esta forma, hay una secante para cada punto
. De esta forma, hay una secante para cada punto
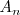 . Sea
. Sea
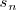 la recta que pasa por
la recta que pasa por
 y por
y por
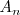 .
.
Cuando
 tiende a
tiende a
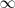 ,
,
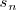 tiende a la tangente a la grafica de la función
tiende a la tangente a la grafica de la función
 en el punto
en el punto
 ,
,
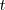 :
:
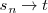
Habria de esperar, pues, que la pendiente de
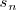 tienda a la pendiente de
tienda a la pendiente de
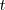 cuando
cuando
 tiende a
tiende a
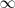 . Como la pendiente de
. Como la pendiente de
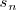 es una tasa de variación
media:
es una tasa de variación
media:
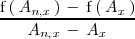
su limite cuando
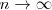 es una tasa de variación instantánea, la derivada de
es una tasa de variación instantánea, la derivada de
 en
en
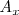 . Es decir la pendiente de
. Es decir la pendiente de
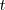 es la derivada de
es la derivada de
 en
en
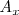 .
.