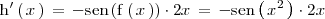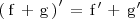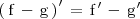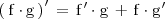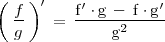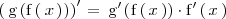Definición de derivada
De Wikillerato
| Línea 1: | Línea 1: | ||
| - | + | La derivada de la función | |
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | en el punto | ||
| + | <math> | ||
| + | x \, = \, a | ||
| + | </math> | ||
| + | , | ||
| + | <math> | ||
| + | \mathrm{f}^\prime | ||
| + | \left( | ||
| + | \, a \, | ||
| + | \right) | ||
| + | </math> | ||
| + | , si existe, es el valor del limite: | ||
<br/> | <br/> | ||
| - | + | <center> | |
<math> | <math> | ||
| - | \mathrm{f} \left( \, | + | \lim_{h \to 0} \frac{\mathrm{f}\left( \, a \, + \, h \, \right) \, - \, |
| + | \mathrm{f} \left( \, a \, \right)}{h} | ||
| + | </math>. | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si | ||
| + | <math> | ||
| + | \mathrm{f}^\prime | ||
| + | \left( | ||
| + | \, a \, | ||
| + | \right) | ||
</math> | </math> | ||
| - | es | + | es un número real, la función |
<math> | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | es derivable en | ||
| + | <math> | ||
| + | x \, = \, a | ||
| + | </math>. | ||
| + | Si | ||
| + | <math> | ||
| + | \mathrm{f}^\prime | ||
\left( | \left( | ||
| - | \, a | + | \, a \, |
\right) | \right) | ||
</math> | </math> | ||
| - | , | + | no es un número real o el límite no existe, la función |
<math> | <math> | ||
| - | + | \mathrm{f} | |
</math> | </math> | ||
| - | | + | no es derivable en dicho punto. |
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Ejemplo== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Calculemos la derivada de | ||
<math> | <math> | ||
| - | + | \mathrm{f} | |
| + | \left( | ||
| + | \, x \, | ||
| + | \right) | ||
| + | \, = \, x^2 | ||
</math> | </math> | ||
| - | , | + | en |
| + | <math> | ||
| + | x \, = \, 2 | ||
| + | </math>: | ||
<br/> | <br/> | ||
| Línea 27: | Línea 78: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \frac{\mathrm{f}\left( \, | + | \mathrm{f}^\prime |
| - | + | \left( | |
| + | \, 2 \, | ||
| + | \right) | ||
| + | \, = \, \lim_{h \to 0} \frac{\mathrm{f}\left( \, 2 \, + \, h \, \right) \, - \, | ||
| + | \mathrm{f} \left( \, 2 \, \right)}{h} \, = \, \lim_{h \to 0} \frac | ||
| + | {\left( \, 2 \, + \, h \, \right)^2 \, - \, 2^2}{h} \, = \, | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | \, = \, \lim_{h \to 0} | ||
| + | \frac {\left( \, 4 \, + \, 4h \, + \, h^2 \, \right) \, - \, 4}{h} \, = \, | ||
| + | \lim_{h \to 0} \frac {4h \, + \, h^2}{h} \, = \, \lim_{h \to 0} | ||
| + | \left( | ||
| + | \, h \, + 4 \, \, | ||
| + | \right) | ||
| + | \, = \, 4 | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 34: | Línea 102: | ||
<br/> | <br/> | ||
| - | + | [[Category:Matemáticas]] | |
| + | |||
| + | %% }}} | ||
| + | %% {{{ =tasas de variación | ||
| + | |||
| + | ==Tasa de variación media== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Supongamos que un coche de fórmula uno se mueve en una carretera totalmente recta. A | ||
| + | distintas distancias de la salida se registran los tiempos de paso, obteniendose la | ||
| + | siguiente tabla: | ||
<br/> | <br/> | ||
<center> | <center> | ||
| - | [[Imagen: | + | [[Imagen:tabla7.png]] |
</center> | </center> | ||
<br/> | <br/> | ||
| - | + | En este caso, la posición, | |
| - | + | <math> | |
| + | y | ||
| + | </math> | ||
| + | , se puede ver como una función, | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | , del tiempo, | ||
| + | <math> | ||
| + | x | ||
| + | </math>; es decir: | ||
<br/> | <br/> | ||
| Línea 51: | Línea 140: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | y \, = \, \mathrm{f} \left( \, x \, \right) | |
| - | + | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 58: | Línea 146: | ||
<br/> | <br/> | ||
| - | + | La '''''tasa de variación media''''' de la posición en el intervalo de tiempo desde el | |
| + | instante | ||
<math> | <math> | ||
| - | + | 9 | |
</math> | </math> | ||
| - | | + | al instante |
<math> | <math> | ||
| - | + | 13.4 | |
</math> | </math> | ||
| - | | + | es: |
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
<math> | <math> | ||
| - | + | \frac{\mathrm{f} \left( \, 13.4 \, \right) \, - \, \mathrm{f} \left( \, 9 \, | |
| + | \right)}{13.4 \, - \, 9} \, = \, \frac{6.7 \, - \, 4.5}{13.4 \, - \, 9} \, = \, 0.5 | ||
</math> | </math> | ||
| - | + | </center> | |
| + | |||
| + | <br/> | ||
| + | |||
| + | En general, la tasa de variación media de la función | ||
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
| - | |||
</math> | </math> | ||
| - | | + | en |
<math> | <math> | ||
| - | \left | + | \left[ |
| - | \, | + | \, a, \, b \, |
| - | \right | + | \right] |
| - | </math> | + | </math> |
| + | se define como el cociente: | ||
<br/> | <br/> | ||
| - | + | <center> | |
<math> | <math> | ||
| - | \mathrm{f} | + | \frac{\mathrm{f} \left( \, b \, \right) \, - \, \mathrm{f} \left( \, a \, |
| + | \right)}{b \, - \, a} | ||
</math> | </math> | ||
| - | | + | </center> |
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Tasa de variación instantánea== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La '''''tasa de variación instantánea''''' de la función | ||
| + | <math> | ||
| + | f | ||
| + | </math> | ||
| + | en el punto | ||
<math> | <math> | ||
x \, = \, a | x \, = \, a | ||
</math> | </math> | ||
| - | | + | se obtiene haciendo tender |
| + | <math> | ||
| + | b | ||
| + | </math> | ||
| + | a | ||
| + | <math> | ||
| + | a | ||
| + | </math> | ||
| + | en la '''''tasa de variación media''''' de la función | ||
| + | <math> | ||
| + | f | ||
| + | </math> | ||
| + | en el intervalo | ||
| + | <math> | ||
| + | \left[ | ||
| + | \, a, \, b \, | ||
| + | \right] | ||
| + | </math>; por tanto, la '''''tasa de variación instantánea''''' de la función | ||
<math> | <math> | ||
f | f | ||
</math> | </math> | ||
| - | | + | en el punto |
<math> | <math> | ||
x \, = \, a | x \, = \, a | ||
</math> | </math> | ||
| - | + | es | |
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
<math> | <math> | ||
| - | \mathrm{f} | + | \lim_{h \to 0}\frac{\mathrm{f}\left( \, a \, + \, h \, \right) \, - \, \mathrm{f}\left( \, a \, \right)}{h} |
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | que es precisamente la [[Definición de derivada|derivada]] de la función | ||
| + | <math> | ||
| + | f | ||
| + | </math> | ||
| + | en el punto | ||
| + | <math> | ||
| + | x \, = \, a | ||
</math>. | </math>. | ||
<br/> | <br/> | ||
| - | = | + | NOTA: En el límite anterior |
| + | <math> | ||
| + | b \, = \, a \, + \, h | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | + | [[Category:Matemáticas]] | |
| + | |||
| + | %% }}} | ||
| + | %% {{{ =Derivadas de las funciones elementales | ||
| + | |||
| + | <center> | ||
| + | [[Imagen:tablaDeDerivadas.png]] | ||
| + | </center> | ||
| + | |||
| + | %% }}} | ||
| + | %% {{{ =función derivada | ||
| + | |||
| + | Si | ||
<math> | <math> | ||
| - | \mathrm{f} | + | \mathrm{f} |
</math> | </math> | ||
| - | es | + | es una función derivable en el intervalo |
<math> | <math> | ||
| + | \left( | ||
| + | \, a, \, b \, | ||
| + | \right) | ||
| + | \subset R | ||
| + | </math> | ||
| + | , la '''''función derivada''''' de | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | es la que a cada | ||
| + | <math> | ||
| + | x \in | ||
\left( | \left( | ||
\, a, \, b \, | \, a, \, b \, | ||
\right) | \right) | ||
</math> | </math> | ||
| - | + | le hace corresponder la [[Definición de derivada|derivada]] de | |
<math> | <math> | ||
| - | + | \mathrm{f} | |
</math> | </math> | ||
| - | | + | en dicho punto. Esta función se designa por |
<math> | <math> | ||
| - | + | \mathrm{f}^\prime \left( \, x \, \right) | |
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Una función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | es '''''derivable''''' en el intervalo | ||
| + | <math> | ||
| + | \left( | ||
| + | \, a, \, b \, | ||
| + | \right) | ||
</math> | </math> | ||
| - | + | si lo es en cada punto del intervalo. | |
<br/> | <br/> | ||
| - | + | Llamamos '''''derivada de segundo orden''''' de | |
<math> | <math> | ||
| - | + | \mathrm{f} | |
| - | + | ||
</math> | </math> | ||
| - | </ | + | a la función derivada de |
| + | <math> | ||
| + | \mathrm{f}^\prime | ||
| + | </math>. | ||
| + | Esta función se denota por | ||
| + | <math> | ||
| + | \mathrm{f}^{\prime \prime} | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | + | <math> | |
| + | \mathrm{f}^{\prime \prime \prime} | ||
| + | </math> | ||
| + | es la '''''derivada tercera''''' de | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | y, en general, | ||
| + | <math> | ||
| + | \mathrm{f}^{\left( \, n \, \right)} | ||
| + | </math> | ||
| + | es la '''''derivada n-ésima''''' de | ||
| + | <math> | ||
| + | \mathrm{f} \left( \, x \, \right) | ||
| + | </math>: | ||
| + | <math> | ||
| + | \mathrm{f}^{\left( \, n \, \right)} | ||
| + | </math> | ||
| + | es la función derivada de | ||
| + | <math> | ||
| + | \mathrm{f}^{\left( \, n \, - \, 1 \, \right)} | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | + | [[Category:Matemáticas]] | |
| + | |||
| + | %% }}} | ||
| + | %% {{{ =significado geométrico de la derivada | ||
| + | |||
| + | Consideremos la grafica de una función | ||
<math> | <math> | ||
| - | \mathrm{f} | + | \mathrm{f} |
</math> | </math> | ||
| - | + | . Tomemos un punto | |
<math> | <math> | ||
| + | A \, = \, | ||
\left( | \left( | ||
| - | \, | + | \, A_x, \, \mathrm{f} \left( \, A_x \, \right) \, |
\right) | \right) | ||
</math> | </math> | ||
| - | + | en dicha grafica y consideremos una sucesión de puntos | |
<math> | <math> | ||
| - | + | A_1, \, A_2, \, A_3, \, \ldots | |
</math> | </math> | ||
| - | | + | en la grafica de |
<math> | <math> | ||
| - | + | \mathrm{f} | |
</math> | </math> | ||
| - | + | . Supongamos que todos estos puntos estan a la derecha de | |
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | y que cuando | ||
| + | <math> | ||
| + | n \to \infty | ||
| + | </math> | ||
| + | , | ||
| + | <math> | ||
| + | A_n \to A | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | + | La recta que pasa por los puntos | |
<math> | <math> | ||
| - | + | A | |
| - | + | ||
</math> | </math> | ||
| - | </ | + | y |
| + | <math> | ||
| + | A_n | ||
| + | </math> | ||
| + | es una secante a la grafica de la función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math>. De esta forma, hay una secante para cada punto | ||
| + | <math> | ||
| + | A_n | ||
| + | </math>. Sea | ||
| + | <math> | ||
| + | s_n | ||
| + | </math> | ||
| + | la recta que pasa por | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | y por | ||
| + | <math> | ||
| + | A_n | ||
| + | </math> | ||
| + | . | ||
<br/> | <br/> | ||
| - | + | <center> | |
| + | [[Imagen:tangente.png]] | ||
| + | </center> | ||
<br/> | <br/> | ||
| + | Cuando | ||
| + | <math> | ||
| + | n | ||
| + | </math> | ||
| + | tiende a | ||
| + | <math> | ||
| + | \infty | ||
| + | </math> | ||
| + | , | ||
| + | <math> | ||
| + | s_n | ||
| + | </math> | ||
| + | tiende a la tangente a la grafica de la función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | en el punto | ||
| + | <math> | ||
| + | A | ||
| + | </math>, | ||
| + | <math> | ||
| + | t | ||
| + | </math>: | ||
| + | |||
| + | <br/> | ||
| + | |||
<center> | <center> | ||
| - | + | <math> | |
| + | s_n \to t | ||
| + | </math> | ||
</center> | </center> | ||
<br/> | <br/> | ||
| - | + | Habria de esperar, pues, que la pendiente de | |
| - | + | <math> | |
| + | s_n | ||
| + | </math> | ||
| + | tienda a la pendiente de | ||
| + | <math> | ||
| + | t | ||
| + | </math> | ||
| + | cuando | ||
| + | <math> | ||
| + | n | ||
| + | </math> | ||
| + | tiende a | ||
| + | <math> | ||
| + | \infty | ||
| + | </math>. Como la pendiente de | ||
| + | <math> | ||
| + | s_n | ||
| + | </math> | ||
| + | es una [[La derivada como una tasa de variación instantánea|tasa de variación | ||
| + | media]]: | ||
| + | |||
| + | <br/> | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \frac{\mathrm{f} \left( \, A_{n,x} \, \right) \, - \, \mathrm{f} \left( \, A_x \, | |
| - | \mathrm{f} \left( \, | + | \right)}{A_{n,x} \, - \, A_x} |
</math> | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | (<math> | ||
| + | A_{n,x} \, = | ||
| + | </math> | ||
| + | abcisa de | ||
| + | <math> | ||
| + | A_n | ||
| + | </math>) | ||
</center> | </center> | ||
<br/> | <br/> | ||
| - | + | su limite cuando | |
<math> | <math> | ||
| - | + | n \to \infty | |
</math> | </math> | ||
| - | es | + | es una [[La derivada como una tasa de variación instantánea|tasa de variación instantánea]], la [[Definición de derivada|derivada]] de |
<math> | <math> | ||
| - | + | \mathrm{f} | |
</math> | </math> | ||
| - | | + | en |
<math> | <math> | ||
| - | + | A_x | |
| + | </math>; es decir la pendiente de | ||
| + | <math> | ||
| + | t | ||
</math> | </math> | ||
| - | | + | es la derivada de |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
| - | |||
</math> | </math> | ||
| - | | + | en |
<math> | <math> | ||
| - | + | A_x | |
| - | + | ||
| - | + | ||
</math>. | </math>. | ||
<br/> | <br/> | ||
| - | + | [[Category:Matemáticas]] | |
| + | |||
| + | %% }}} | ||
| + | %% {{{ =función derivada de las operaciones de funciones | ||
| + | |||
| + | __TOC__ | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Derivada de la suma== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La [[Función derivada y derivadas sucesivas|derivada]] de la suma de dos funciones es | ||
| + | igual a la suma de las derivadas de dichas funciones: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \, \mathrm{f} \, + \, \mathrm{g} \, | ||
| + | \right) | ||
| + | ^\prime \, = \, \mathrm{f}^\prime \, + \, \mathrm{g}^\prime \, | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Este resultado, se puede ampliar a cualquier número de funciones. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Derivada de la diferencia== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La [[Función derivada y derivadas sucesivas|derivada]] de la diferencia de dos funciones es | ||
| + | igual a la diferencia de las derivadas de dichas funciones: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \, \mathrm{f} \, - \, \mathrm{g} \, | ||
| + | \right) | ||
| + | ^\prime \, = \, \mathrm{f}^\prime \, - \, \mathrm{g}^\prime \, | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Derivada del producto== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La [[Función derivada y derivadas sucesivas|derivada]] del producto de dos funciones, | ||
| + | | ||
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | | + | y |
<math> | <math> | ||
| - | + | \mathrm{g} | |
| + | </math> | ||
| + | , viene dada por la fórmula: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \, \mathrm{f} \cdot \mathrm{g} \, | ||
| + | \right) | ||
| + | ^\prime \, = \, \mathrm{f}^\prime \cdot \mathrm{g} \, + \, \mathrm{f} \cdot \mathrm{g}^\prime \, | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Derivada del cociente== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La [[Función derivada y derivadas sucesivas|derivada]] del cociente | ||
| + | <math> | ||
| + | \frac{f}{g} | ||
| + | </math> | ||
| + | viene dada por la fórmula: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \, \frac{f}{g} \, | ||
| + | \right) | ||
| + | ^\prime \, = \, \frac{\mathrm{f}^\prime \cdot \mathrm{g} \, - \, \mathrm{f} \cdot \mathrm{g}^\prime}{\mathrm{g}^2} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | [[Category:Matemáticas]] | ||
| + | |||
| + | %% }}} | ||
| + | %% {{{ =composición de funciones | ||
| + | |||
| + | El componer dos funciones | ||
| + | <math> | ||
| + | \mathrm{f} | ||
</math> | </math> | ||
y | y | ||
<math> | <math> | ||
| - | + | \mathrm{g} | |
</math> | </math> | ||
| - | | + | consiste en aplicar |
<math> | <math> | ||
| - | + | g | |
</math> | </math> | ||
| - | + | al resultado de calcular | |
<math> | <math> | ||
| - | \mathrm{f} | + | \mathrm{f} \left( \, x \, \right) |
| - | </math> | + | </math> |
| + | , es decir: | ||
<br/> | <br/> | ||
| - | + | <center> | |
| + | <math> | ||
| + | R \stackrel{\mathrm{f}}{\longrightarrow} R \stackrel{\mathrm{g}}{\longrightarrow} R | ||
| + | </math> | ||
<br/> | <br/> | ||
| - | |||
<math> | <math> | ||
| - | \mathrm{f} \left( \, x \, \right) | + | x \longrightarrow \mathrm{f} \left( \, x \, \right) \longrightarrow \mathrm{g} |
| + | \left( \mathrm{f} \left( \, x \, \right) \right) | ||
</math> | </math> | ||
| - | + | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La [[Función derivada y derivadas sucesivas|derivada]] de | ||
<math> | <math> | ||
| - | \left( | + | \mathrm{g} \left( \mathrm{f} \left( \, x \, \right) \right) |
| - | + | ||
| - | \right) | + | |
</math> | </math> | ||
| - | + | viene dada por la fórmula: | |
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \, \mathrm{g} \left( \mathrm{f} \left( \, x \, \right) \right) | ||
| + | \right) | ||
| + | ^\prime \, = \, \mathrm{g}^\prime \left( \mathrm{f} \left( \, x \, \right) \right) \cdot \mathrm{f}^\prime \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | resultado que se conoce como '''''regla de la cadena'''''. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Ejemplo== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Calculemos la derivada de | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
<math> | <math> | ||
| - | + | \mathrm{h} \left( \, x \, \right) \, = \, \cos \left( \, x^2 \, \right) | |
</math> | </math> | ||
| - | + | </center> | |
| + | |||
| + | <br/> | ||
| + | |||
| + | | ||
<math> | <math> | ||
| - | + | \mathrm{h} | |
</math> | </math> | ||
| - | , se | + | es la composición de dos funciones: |
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left\{ | ||
| + | \begin{array}[c]{rcl} | ||
| + | \mathrm{f} \left( \, x \, \right) \, & = & \, x^2 | ||
| + | \\ | ||
| + | \mathrm{g} \left( \, x \, \right) \, & = & \, \cos \left( \, x \, \right) | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Es decir | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{h} \left( \, x \, \right) \, = \, \mathrm{g} \left( \, \mathrm{f} \left( \, x \, \right) \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para derivar | ||
| + | <math> | ||
| + | \mathrm{h} \left( \, x \, \right) | ||
| + | </math> | ||
| + | utilizamos la regla de la cadena: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{h}^\prime \left( \, x \, \right) \, = \, \mathrm{g}^\prime \left( \, \mathrm{f} \left( \, x \, \right) \right) \cdot \mathrm{f}^\prime \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Como | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left\{ | ||
| + | \begin{array}[c]{rcl} | ||
| + | \mathrm{f}^\prime \left( \, x \, \right) \, & = & \, 2x | ||
| + | \\ | ||
| + | \mathrm{g}^\prime \left( \, x \, \right) \, & = & \, -\mathrm{sen} \left( \, x \, \right) | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | se tiene que | ||
<br/> | <br/> | ||
| Línea 276: | Línea 793: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \mathrm{h}^\prime \left( \, x \, \right) \, = \, -\mathrm{sen} \left( | |
| - | \, | + | \mathrm{f} \left( \, x \, \right) \right) \cdot 2x \, = \, -\mathrm{sen} \left( |
| + | \, x^2 \, \right) \cdot 2x | ||
</math> | </math> | ||
</center> | </center> | ||
Revisión de 01:38 15 ene 2007
La derivada de la función
 en el punto
en el punto
 ,
,
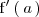 , si existe, es el valor del limite:
, si existe, es el valor del limite:
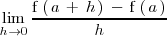 .
.
Si
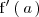 es un número real, la función
es un número real, la función
 es derivable en
es derivable en
 .
Si
.
Si
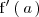 no es un número real o el límite no existe, la función
no es un número real o el límite no existe, la función
 no es derivable en dicho punto.
no es derivable en dicho punto.
Ejemplo
Calculemos la derivada de
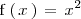 en
en
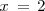 :
:
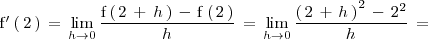
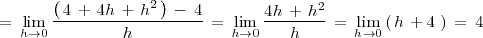
%% }}} %% {{{ =tasas de variación
Tasa de variación media
Supongamos que un coche de fórmula uno se mueve en una carretera totalmente recta. A distintas distancias de la salida se registran los tiempos de paso, obteniendose la siguiente tabla:
En este caso, la posición,
 , se puede ver como una función,
, se puede ver como una función,
 , del tiempo,
, del tiempo,
 ; es decir:
; es decir:
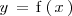
La tasa de variación media de la posición en el intervalo de tiempo desde el
instante
 al instante
al instante
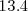 es:
es:
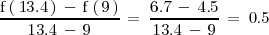
En general, la tasa de variación media de la función
 en
en
![\left[
</p>
<pre> \, a, \, b \,
</pre>
<p>\right]
\left[
</p>
<pre> \, a, \, b \,
</pre>
<p>\right]](/images/math/math-8e146dde08a38232680af38266cb8d8c.png) se define como el cociente:
se define como el cociente:
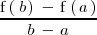
Tasa de variación instantánea
La tasa de variación instantánea de la función
 en el punto
en el punto
 se obtiene haciendo tender
se obtiene haciendo tender
 a
a
 en la tasa de variación media de la función
en la tasa de variación media de la función
 en el intervalo
en el intervalo
![\left[
</p>
<pre> \, a, \, b \,
</pre>
<p>\right]
\left[
</p>
<pre> \, a, \, b \,
</pre>
<p>\right]](/images/math/math-8e146dde08a38232680af38266cb8d8c.png) ; por tanto, la tasa de variación instantánea de la función
; por tanto, la tasa de variación instantánea de la función
 en el punto
en el punto
 es
es
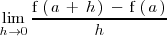
que es precisamente la derivada de la función
 en el punto
en el punto
 .
.
NOTA: En el límite anterior
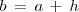 .
.
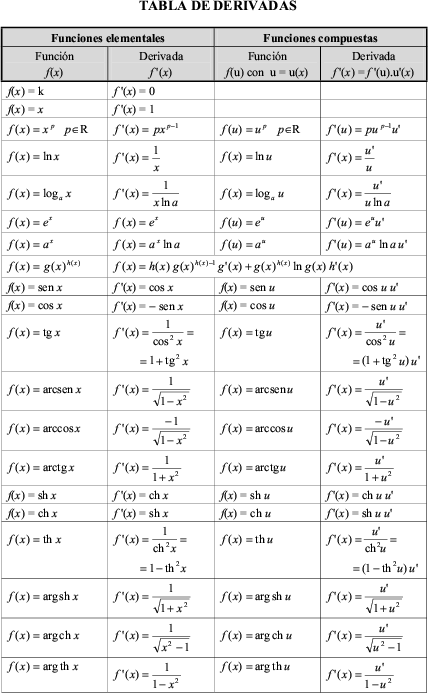
%% }}} %% {{{ =Derivadas de las funciones elementales
%% }}} %% {{{ =función derivada
Si
 es una función derivable en el intervalo
es una función derivable en el intervalo
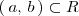 , la función derivada de
, la función derivada de
 es la que a cada
es la que a cada
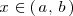 le hace corresponder la derivada de
le hace corresponder la derivada de
 en dicho punto. Esta función se designa por
en dicho punto. Esta función se designa por
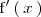 .
.
Una función
 es derivable en el intervalo
es derivable en el intervalo
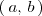 si lo es en cada punto del intervalo.
si lo es en cada punto del intervalo.
Llamamos derivada de segundo orden de
 a la función derivada de
a la función derivada de
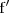 .
Esta función se denota por
.
Esta función se denota por
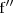 .
.
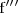 es la derivada tercera de
es la derivada tercera de
 y, en general,
y, en general,
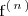 es la derivada n-ésima de
es la derivada n-ésima de
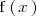 :
:
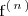 es la función derivada de
es la función derivada de
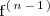 .
.
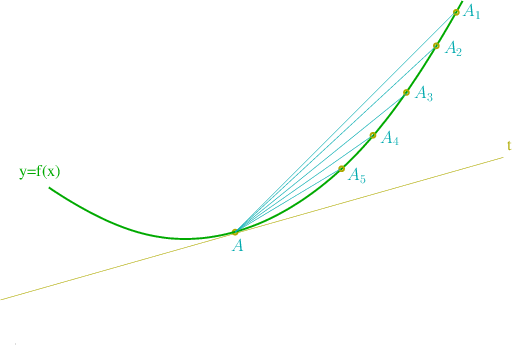
%% }}} %% {{{ =significado geométrico de la derivada
Consideremos la grafica de una función
 . Tomemos un punto
. Tomemos un punto
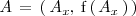 en dicha grafica y consideremos una sucesión de puntos
en dicha grafica y consideremos una sucesión de puntos
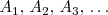 en la grafica de
en la grafica de
 . Supongamos que todos estos puntos estan a la derecha de
. Supongamos que todos estos puntos estan a la derecha de
 y que cuando
y que cuando
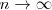 ,
,
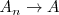 .
.
La recta que pasa por los puntos
 y
y
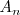 es una secante a la grafica de la función
es una secante a la grafica de la función
 . De esta forma, hay una secante para cada punto
. De esta forma, hay una secante para cada punto
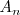 . Sea
. Sea
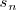 la recta que pasa por
la recta que pasa por
 y por
y por
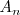 .
.
Cuando
 tiende a
tiende a
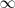 ,
,
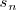 tiende a la tangente a la grafica de la función
tiende a la tangente a la grafica de la función
 en el punto
en el punto
 ,
,
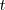 :
:
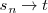
Habria de esperar, pues, que la pendiente de
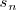 tienda a la pendiente de
tienda a la pendiente de
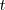 cuando
cuando
 tiende a
tiende a
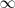 . Como la pendiente de
. Como la pendiente de
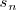 es una tasa de variación
media:
es una tasa de variación
media:
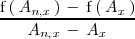
(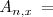 abcisa de
abcisa de
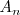 )
)
su limite cuando
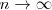 es una tasa de variación instantánea, la derivada de
es una tasa de variación instantánea, la derivada de
 en
en
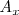 ; es decir la pendiente de
; es decir la pendiente de
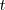 es la derivada de
es la derivada de
 en
en
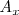 .
.
%% }}} %% {{{ =función derivada de las operaciones de funciones
Tabla de contenidos |
Derivada de la suma
La derivada de la suma de dos funciones es igual a la suma de las derivadas de dichas funciones:
Este resultado, se puede ampliar a cualquier número de funciones.
Derivada de la diferencia
La derivada de la diferencia de dos funciones es igual a la diferencia de las derivadas de dichas funciones:
Derivada del producto
La derivada del producto de dos funciones,
 y
y
 , viene dada por la fórmula:
, viene dada por la fórmula:
Derivada del cociente
La derivada del cociente
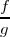 viene dada por la fórmula:
viene dada por la fórmula:
%% }}} %% {{{ =composición de funciones
El componer dos funciones
 y
y
 consiste en aplicar
consiste en aplicar
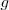 al resultado de calcular
al resultado de calcular
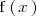 , es decir:
, es decir:
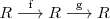
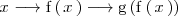
La derivada de
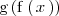 viene dada por la fórmula:
viene dada por la fórmula:
resultado que se conoce como regla de la cadena.
Ejemplo
Calculemos la derivada de
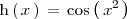
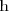 es la composición de dos funciones:
es la composición de dos funciones:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{f} \left( \, x \, \right) \, & = & \, x^2
\\
\mathrm{g} \left( \, x \, \right) \, & = & \, \cos \left( \, x \, \right)
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{f} \left( \, x \, \right) \, & = & \, x^2
\\
\mathrm{g} \left( \, x \, \right) \, & = & \, \cos \left( \, x \, \right)
\end{array}
</pre>
<p>\right.](/images/math/math-693d66707eee4ea00c554a821a1e1902.png)
Es decir
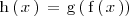
Para derivar
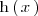 utilizamos la regla de la cadena:
utilizamos la regla de la cadena:
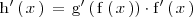
Como
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{f}^\prime \left( \, x \, \right) \, & = & \, 2x
\\
\mathrm{g}^\prime \left( \, x \, \right) \, & = & \, -\mathrm{sen} \left( \, x \, \right)
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{f}^\prime \left( \, x \, \right) \, & = & \, 2x
\\
\mathrm{g}^\prime \left( \, x \, \right) \, & = & \, -\mathrm{sen} \left( \, x \, \right)
\end{array}
</pre>
<p>\right.](/images/math/math-87d2e3c97615febe5a00ed62cd9f55bb.png)
se tiene que