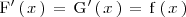Navegación
Herramientas
Primitiva de una función
De Wikillerato
| Línea 177: | Línea 177: | ||
\mathrm{G} \left( \, x \, \right) \, = \, x^2 \, + \, 7 | \mathrm{G} \left( \, x \, \right) \, = \, x^2 \, + \, 7 | ||
</math> | </math> | ||
| - | son | + | son dos funciones primitivas de |
<math> | <math> | ||
\mathrm{f} \left( \, x \, \right) \, = \, 2 \cdot x | \mathrm{f} \left( \, x \, \right) \, = \, 2 \cdot x | ||
Revisión de 15:48 10 mar 2008
Tabla de contenidos[ocultar] |
Definición
Dadas dos funciones
y
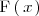, definidas en un intervalo
![</p>
<pre>I =
</pre>
<p>\left[
</p>
<pre> \, a, \, b \,
</pre>
<p>\right]](/images/math/math-ec1b2022a1621b88d0396b296196a49e.png "</p>
<pre>I =
</pre>
<p>\left[
</p>
<pre> \, a, \, b \,
</pre>
<p>\right]")
, diremos que
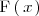es una función primitiva de
si la derivada de
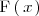es la función
en el intervalo
.
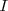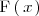es primitiva de
en
[Unparseable or potentially dangerous latex formula. Error 3 ]
Calcular la primitiva de una función es el proceso inverso al de calcular su derivada.
Ejemplo
Consideremos la función
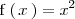y denotemos por
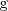la derivada de
, es decir:
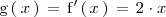
Entonces una primitiva de
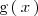es
.
¿Cuantas primitivas puede tener una función?
Una función cualquiera admite infinitas primitivas, de hecho
Dos funciones son primitivas de una misma función si y solo si se diferencian solo en una constante aditiva.
Es decir, si
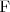y
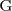son primitivas de
, entonces existe un número real
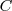, tal que
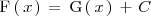
Reciprocamente, si a una primitiva de una fución
le añadimos una constante
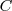, entonces obtenemos otra primitiva de
.
Ejemplo
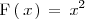y
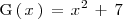son dos funciones primitivas de
[Unparseable or potentially dangerous latex formula. Error 3 ]
, ya que
Tweet
