Navegación
Sistemas axonométricos ortogonales y oblicuos
De Wikillerato
Revisión de 08:42 29 jul 2008
Fundamento del sistema
Los sistemas axonométricos están basados en la proyección cilíndrica de los objetos sobre tres planos de proyección que forman un triedro trirrectángulo y la proyección del objeto y sus tres proyecciones sobre un plano llamado plano del cuadro. Por lo tanto cada objeto tiene cuatro proyecciones, la directa y las proyecciones sobre el plano horizontal y los dos verticales. Además esto implica la aparición de coeficientes de reducción que son razón entre la magnitud del segmento proyectado en cada plano y la del segmento real.
Los sistemas axonométricos ortogonales se basan en la proyección cilíndrica ortogonal. Son las axonometrías isométrica, dimétricas y trimétricas.
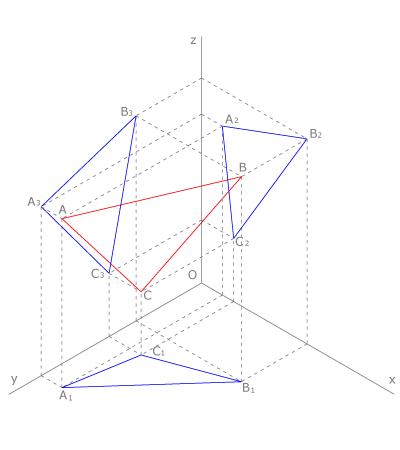
En la figura vemos la representación isométrica de un triángulo 
que se proyecta sobre el primer plano vertical como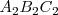 
, sobre el segundo plano vertical como 
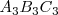y sobre el plano horizontal como 
.
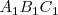Los sistemas axonométricos oblicuos se basan en la proyección cilíndrica oblicua o paralela, como las perspectivas caballera y militar.
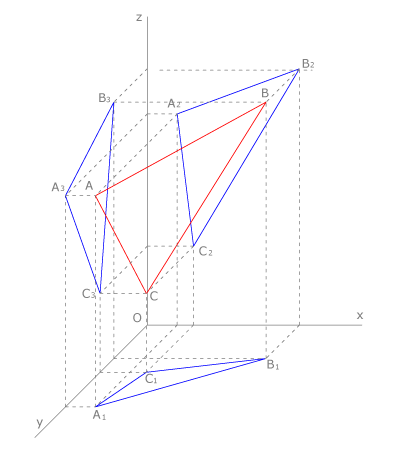
En la figura vemos la representación caballera de un triángulo que se proyecta sobre el primer plano vertical como 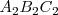, sobre el segundo plano vertical como 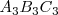y sobre el plano horizontal como .
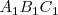Métodos operativos
Son los métodos geométricos que aplicaremos a las características de los sistemas axonométricos.
Resolución de problemas
Se trata de resolver problemas básicos de representación, intersecciones con rectas y planos y verdaderas magnitudes.
Tweet
